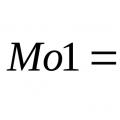The static calculation of engineering structures in many cases comes down to the consideration of the equilibrium conditions of a structure consisting of a system of bodies connected by some kind of connections. The connections connecting the parts of this structure will be called internal Unlike external connections connecting the structure to bodies not included in it (for example, to supports).
If, after discarding external connections (supports), the structure remains rigid, then statics problems are solved for it as for an absolutely rigid body. However, there may be engineering structures that do not remain rigid after discarding external connections. An example of such a design is a three-hinged arch. If we discard supports A and B, then the arch will not be rigid: its parts can rotate around hinge C.
Based on the principle of solidification, the system of forces acting on such a structure must, in equilibrium, satisfy the equilibrium conditions of a solid body. But these conditions, as indicated, while necessary, will not be sufficient; therefore, it is impossible to determine all unknown quantities from them. To solve the problem, it is necessary to additionally consider the equilibrium of one or more parts of the structure.
For example, by composing equilibrium conditions for the forces acting on a three-hinged arch, we obtain three equations with four unknowns X A, Y A, X B, Y B . Having additionally considered the equilibrium conditions of the left (or right) half of it, we obtain three more equations containing two new unknowns X C, Y C, in Fig. 61 not shown. By solving the resulting system of six equations, we find all six unknowns.
14. Special cases of reduction of a spatial system of forces
If, when bringing a system of forces to a dynamic screw, the main moment of the dynamo turns out to be equal to zero, and the main vector is different from zero, then this means that the system of forces is reduced to a resultant, and the central axis is the line of action of this resultant. Let us find out under what conditions related to the main vector Fp and the main moment M 0 this can happen. Since the main moment of the dynamism M* is equal to the component of the main moment M 0 directed along the main vector, the considered case M* = O means that the main moment M 0 is perpendicular to the main vector, i.e. / 2 = Fo*M 0 = 0. It immediately follows that if the main vector F 0 is not equal to zero, and the second invariant is equal to zero, Fo≠O, / 2 = F 0 *M 0 =0, (7.9) then the considered the system is reduced to the resultant.
In particular, if for any reduction center F 0 ≠0, and M 0 = 0, then this means that the system of forces is reduced to a resultant passing through this reduction center; in this case, condition (7.9) will also be satisfied. Let us generalize the theorem on the moment of the resultant (Varignon’s theorem) given in Chapter V to the case of a spatial system of forces. If the spatial system.
forces are reduced to a resultant, then the moment of the resultant relative to an arbitrary point is equal to the geometric sum of the moments of all forces relative to the same point. P 
Let the system of forces have a resultant R and a point ABOUT lies on the line of action of this resultant. If we bring a given system of forces to this point, we obtain that the main moment is equal to zero. 
Let's take some other reduction center O1; (7.10)C 
on the other hand, based on formula (4.14) we haveMo1=Mo+Mo1(Fo), (7.11) since M 0 = 0. Comparing expressions (7.10) and (7.11) and taking into account that in this case F 0 = R, we obtain (7.12).
Thus, the theorem is proven.
Let, for any choice of the reduction center, Fo=O, M ≠0. Since the main vector does not depend on the reduction center, it is equal to zero for any other choice of the reduction center. Therefore, the main moment also does not change when the center of reduction changes, and, therefore, in this case the system of forces is reduced to a pair of forces with a moment equal to M0.
Let us now compile a table of all possible cases of reduction of the spatial system of forces:
If all the forces are in the same plane, for example, in the plane Ooh, then their projections onto the axis G and moments about the axes X And at will be equal to zero. Therefore, Fz=0; Mox=0, Moy=0. Introducing these values into formula (7.5), we find that the second invariant of a plane system of forces is equal to zero. We obtain the same result for a spatial system of parallel forces. Indeed, let all forces be parallel to the axis z. Then their projections on the axis X And at and the moments about the z axis will be equal to 0. Fx=0, Fy=0, Moz=0
Based on what has been proven, it can be argued that a plane system of forces and a system of parallel forces are not reduced to a dynamic screw.
1
1.
Equilibrium of a body in the presence of sliding friction If two bodies / and // (Fig. 6.1) interact with each other, touching at a point A, then the reaction R A, acting, for example, from the side of the body // and applied to the body /, can always be decomposed into two components: N.4, directed along the common normal to the surface of the contacting bodies at point A, and T 4, lying in the tangent plane . Component N.4 is called normal reaction force T l is called sliding friction force - it prevents the body from sliding / along the body //. In accordance with the axiom 4
(Newton's 3rd z-on) a reaction force of equal magnitude and opposite direction acts on the body // from the side of the body /. Its component perpendicular to the tangent plane is called force of normal pressure. As mentioned above, the friction force T A
=
Oh, if the contacting surfaces are perfectly smooth. In real conditions, surfaces are rough and in many cases the friction force cannot be neglected. To clarify the basic properties of friction forces, we will carry out an experiment according to the scheme presented in Fig. 6.2, A. To body 5, located on a stationary plate D, is attached a thread thrown over block C, the free end of which is equipped with a support platform A. If the pad A gradually load, then with an increase in its total weight the thread tension will increase S,
which tends to move the body to the right. However, as long as the total load is not too great, the frictional force T will hold the body IN at rest. In Fig. 6.2, b acts on the body are depicted IN forces, and P denotes the force of gravity, and N denotes the normal reaction of the plate D.
If the load is insufficient to break the rest, the following equilibrium equations are valid: N-
P
= 0,
(6.1) S-T = 0. (6.2). It follows from this that N
=
PAnd T = S. Thus, while the body is at rest, the friction force remains equal to the tension force of the thread S. Let us denote by Tmax
friction force at the critical moment of the loading process, when the body IN loses balance and begins to slide on the slab D.
Therefore, if the body is in equilibrium, then T≤Tmax.Maximum friction force T tah
depends on the properties of the materials from which the bodies are made, their condition (for example, on the nature of surface treatment), as well as on the value of normal pressure N. As experience shows, the maximum friction force is approximately proportional to normal pressure, i.e. e. there is equality Tmax=
fN.
(6.4). This relation is called Amonton-Coulomb law. The dimensionless coefficient / is called sliding friction coefficient. As follows from experience, it the value does not depend within wide limits on the area of contacting surfaces, but depends on the material and the degree of roughness of the contacting surfaces. The friction coefficient values are determined empirically and can be found in reference tables. Inequality" (6.3) can now be written as T≤fN
(6.5).The case of strict equality in (6.5) corresponds to the maximum value of the friction force. This means that the friction force can be calculated using the formula T
=
fN
only in cases where it is known in advance that a critical incident is occurring. In all other cases, the friction force should be determined from the equilibrium equations. Consider a body located on a rough surface. We will assume that as a result of the action of active forces and reaction forces, the body is in limiting equilibrium. In Fig. 6.6, a
the limiting reaction R and its components N and Tmax are shown (in the position shown in this figure, active forces tend to move the body to the right, the maximum friction force Tmax is directed to the left). Corner f between limit reaction R and the normal to the surface is called the friction angle. Let's find this angle. From Fig. 6.6, and we have tgφ=Tmax/N or, using expression (6.4), tgφ= f (6-7) From this formula it is clear that instead of the friction coefficient, you can set the friction angle (in the reference tables p 
both quantities are given).
The system of forces is called balanced, if under the influence of this system the body remains at rest.
Equilibrium conditions:
The first condition for the equilibrium of a rigid body:
For a rigid body to be in equilibrium, it is necessary that the sum of external forces applied to the body be equal to zero.
The second condition for the equilibrium of a rigid body:
When a rigid body is in equilibrium, the sum of the moments of all external forces acting on it relative to any axis is equal to zero.
General condition for the equilibrium of a rigid body:
For a rigid body to be in equilibrium, the sum of external forces and the sum of moments of forces acting on the body must be zero. The initial velocity of the center of mass and the angular velocity of rotation of the body must also be equal to zero.
Theorem. Three forces balance a rigid body only if they all lie in the same plane.
11. Flat force system– these are forces located in one plane.
Three forms of equilibrium equations for a plane system:
Center of gravity of the body.
Center of gravity A body of finite dimensions is called the point about which the sum of the moments of gravity of all particles of the body is equal to zero. At this point the force of gravity of the body is applied. The center of gravity of a body (or system of forces) usually coincides with the center of mass of the body (or system of forces).
Center of gravity of a flat figure:
A practical method for finding the center of mass of a plane figure: hang the body in a gravity field so that it can freely rotate around the suspension point O1 . In equilibrium the center of mass WITH is on the same vertical with the suspension point (below it), since it is equal to zero
moment of gravity, which can be considered applied at the center of mass. By changing the suspension point, we find another straight line in the same way O 2 C , passing through the center of mass. The position of the center of mass is given by the point of their intersection.
Center of mass speed:
The momentum of a particle system is equal to the product of the mass of the entire system M= Σmi on the speed of its center of mass V :
The center of mass characterizes the movement of the system as a whole.
15. Sliding friction– friction during relative motion of contacting bodies.
Static friction– friction in the absence of relative movement of contacting bodies.
Sliding friction force Ftr between the surfaces of contacting bodies during their relative motion depends on the force of the normal reaction N , or from the force of normal pressure Pn , and Ftr=kN or Ftr=kPn , where k – sliding friction coefficient , depending on the same factors as the static friction coefficient k0 , as well as on the speed of relative motion of the contacting bodies.
16. Rolling friction- This is the rolling of one body over another. The sliding friction force does not depend on the size of the rubbing surfaces, but only on the quality of the surfaces of the rubbing bodies and on the force that reduces the rubbing surfaces and is directed perpendicular to them. F=kN, Where F- friction force, N– the magnitude of the normal reaction and k – sliding friction coefficient.
17. Equilibrium of bodies in the presence of friction- this is the maximum adhesion force proportional to the normal pressure of the body on the plane.
The angle between the total reaction, based on the greatest frictional force for a given normal reaction, and the direction of the normal reaction is called friction angle.
A cone with an apex at the point of application of the normal reaction of a rough surface, the generatrix of which makes an angle of friction with this normal reaction, is called friction cone.
Dynamics.
1. IN dynamics the influence of interactions between bodies on their mechanical motion is considered.
Weight- this is a painting characteristic of a material point. The mass is constant. The mass is adjective (additive)
Force - this is a vector that completely characterizes the interaction of a material point on it with other material points.
Material point– a body whose dimensions and shape are unimportant in the motion under consideration. (ex: in translational motion a rigid body can be considered a material point)
System of material dots called a set of material points interacting with each other.
Newton's 1st law: any material point maintains a state of rest or uniform rectilinear motion until external influences change this state.
Newton's 2nd law: the acceleration acquired by a material point in an inertial reference frame is directly proportional to the force acting on the point, inversely proportional to the mass of the point and coincides in direction with the force: a=F/m
DEFINITION
Stable balance- this is an equilibrium in which a body, removed from a position of equilibrium and left to itself, returns to its previous position.
This occurs if, with a slight displacement of the body in any direction from the original position, the resultant of the forces acting on the body becomes non-zero and is directed towards the equilibrium position. For example, a ball lying at the bottom of a spherical depression (Fig. 1 a).
DEFINITION
Unstable equilibrium- this is an equilibrium in which a body, taken out of an equilibrium position and left to itself, will deviate even more from the equilibrium position.
In this case, with a slight displacement of the body from the equilibrium position, the resultant of the forces applied to it is non-zero and directed from the equilibrium position. An example is a ball located at the top point of a convex spherical surface (Fig. 1 b).
DEFINITION
Indifferent Equilibrium- this is an equilibrium in which a body, taken out of an equilibrium position and left to its own devices, does not change its position (state).
In this case, with small displacements of the body from the original position, the resultant of the forces applied to the body remains equal to zero. For example, a ball lying on a flat surface (Fig. 1c).
Fig.1. Different types of body balance on a support: a) stable balance; b) unstable equilibrium; c) indifferent equilibrium.
Static and dynamic balance of bodies
If, as a result of the action of forces, the body does not receive acceleration, it can be at rest or move uniformly in a straight line. Therefore, we can talk about static and dynamic equilibrium.
DEFINITION
Static balance- this is an equilibrium when, under the influence of applied forces, the body is at rest.
Dynamic balance- this is an equilibrium when, due to the action of forces, the body does not change its movement.
A lantern suspended on cables, or any building structure, is in a state of static equilibrium. As an example of dynamic equilibrium, consider a wheel that rolls on a flat surface in the absence of friction forces.
Statics.
A branch of mechanics that studies the equilibrium conditions of mechanical systems under the influence of forces and moments applied to them.
Balance of power.
Mechanical balance, also known as static equilibrium, is a state of a body at rest or in uniform motion in which the sum of the forces and moments acting on it is zero
Conditions for the equilibrium of a rigid body.
Necessary and sufficient conditions for the equilibrium of a free rigid body are the equality to zero of the vector sum of all external forces acting on the body, the equality to zero of the sum of all moments of external forces relative to an arbitrary axis, the equality to zero of the initial velocity of translational motion of the body and the condition of equality to zero of the initial angular velocity of rotation.
Types of balance.
Body balance is stable, if, for any small deviations from the equilibrium position allowed by external connections, forces or moments of force arise in the system, tending to return the body to its original state.
Body balance is unstable, if at least for some small deviations from the equilibrium position allowed by external connections, forces or moments of forces arise in the system, tending to further deviate the body from the initial state of equilibrium.
The equilibrium of a body is called indifferent, if, for any small deviations from the equilibrium position allowed by external connections, forces or moments of force arise in the system, tending to return the body to its original state
Center of gravity of a rigid body.
Center of gravity body is the point relative to which the total moment of gravity acting on the system is equal to zero. For example, in a system consisting of two identical masses connected by an inflexible rod and placed in a non-uniform gravitational field (for example, a planet), the center of mass will be in the middle of the rod, while the center of gravity of the system will be shifted to the end of the rod that is closer to the planet (since the weight of the mass P = m g depends on the gravitational field parameter g), and, generally speaking, is even located outside the rod.
In a constant parallel (uniform) gravitational field, the center of gravity always coincides with the center of mass. Therefore, in practice, these two centers almost coincide (since the external gravitational field in non-space problems can be considered constant within the volume of the body).
For the same reason, the concepts of center of mass and center of gravity coincide when these terms are used in geometry, statics and similar fields, where its application in comparison with physics can be called metaphorical and where the situation of their equivalence is implicitly assumed (since there is no real gravitational field and it makes sense to take into account its heterogeneity). In these applications, traditionally both terms are synonymous, and often the second is preferred simply because it is older.
