Ecuaciones trigonométricas .
Las ecuaciones trigonométricas más simples. .
Métodos para resolver ecuaciones trigonométricas.
Ecuaciones trigonométricas. Una ecuación que contiene una incógnita bajo el signo de la función trigonométrica se llama trigonométrico.
Las ecuaciones trigonométricas más simples.


Métodos de solución ecuaciones trigonométricas. Resolver una ecuación trigonométrica consta de dos etapas: transformación de ecuación para hacerlo más simple tipo (ver arriba) y soluciónel resultado más simple ecuación trigonométrica. Hay siete Métodos básicos para resolver ecuaciones trigonométricas.
1. Método algebraico. Este método nos resulta bien conocido por el álgebra.
(método de sustitución y sustitución de variables).

2. Factorización. Veamos este método con ejemplos.
Ejemplo 1. Resuelve la ecuación: pecado X+porque X = 1 .
Solución. Movamos todos los términos de la ecuación hacia la izquierda:
Pecado X+porque X – 1 = 0 ,
Transformemos y factoricemos la expresión en
Lado izquierdo de la ecuación:

Ejemplo 2. Resuelve la ecuación: porque 2 X+ pecado X porque X = 1.
Solución: cos 2 X+ pecado X porque X– pecado 2 X– porque 2 X = 0 ,
Pecado X porque X– pecado 2 X = 0 ,
Pecado X· (porque X– pecado X ) = 0 ,

Ejemplo 3. Resuelve la ecuación: porque 2 X–cos 8 X+ porque 6 X = 1.
Solución: cos 2 X+ porque 6 X= 1 + porque 8 X,
2 porque 4 X porque 2 X= 2cos² 4 X ,
porque 4 X · (porque 2 X– porque 4 X) = 0 ,
porque 4 X · 2 pecado 3 X pecado X = 0 ,
1). porque 4 X= 0, 2). pecado 3 X= 0, 3). pecado X = 0 ,
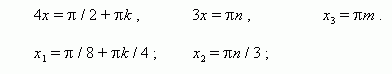
| 3. |
Llevando a ecuación homogénea. La ecuacion llamado homogéneo de acerca de pecado Y porque , Si todo ello términos del mismo grado en relación con pecado Y porque mismo ángulo. Para resolver una ecuación homogénea, necesitas: A) mover todos sus miembros hacia el lado izquierdo; b) sacar todos los factores comunes entre paréntesis; V) igualar todos los factores y paréntesis a cero; GRAMO) paréntesis igual a cero dan ecuación homogénea de menor grado, que debe dividirse en porque(o pecado) en el grado superior; d) resuelve la ecuación algebraica resultante con respecto abroncearse . EJEMPLO Resolver ecuación: 3 pecado 2 X+ 4 pecado X porque X+ 5cos 2 X = 2. Solución: 3 pecado 2 X+ 4 pecado X porque X+ 5 porque 2 X= 2 pecado 2 X+ 2cos 2 X , Pecado 2 X+ 4 pecado X porque X+ 3 porque 2 X = 0 , Bronceado 2 X+ 4 bronceado X + 3 = 0 , de aquí y 2 + 4y +3 = 0 , Las raíces de esta ecuación son:y 1 = - 1, y 2 = - 3, por lo tanto 1) bronceado X= –1, 2) bronceado X = –3, |
4. Transición a medio ángulo. Veamos este método como ejemplo:
EJEMPLO Resolver ecuación: 3 pecado X– 5 porque X = 7.
Solución: 6 pecado ( X/ 2) porque ( X/ 2) – 5 cos² ( X/ 2) + 5 sen² ( X/ 2) =
7 pecado² ( X/ 2) + 7 cos² ( X/ 2) ,
2 pecado² ( X/ 2) – 6 pecado ( X/ 2) porque ( X/ 2) + 12 cos² ( X/ 2) = 0 ,
bronceado²( X/ 2) – 3 bronceado ( X/ 2) + 6 = 0 ,
. . . . . . . . . .
5. Introducción de un ángulo auxiliar. Considere una ecuación de la forma:
a pecado X + b porque X = C ,
Dónde a, b, C– coeficientes;X- desconocido.
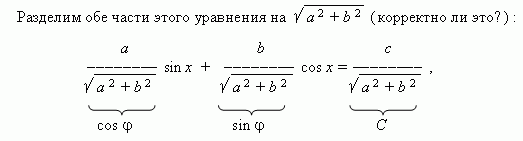
Ahora los coeficientes de la ecuación tienen las propiedades del seno y el coseno, a saber: módulo (valor absoluto) de cada uno
Tarea número 1
La lógica es simple: haremos lo que hicimos antes, ¡sin importar que ahora las funciones trigonométricas tienen un argumento más complejo!
Si tuviéramos que resolver una ecuación de la forma:
Luego escribiríamos la siguiente respuesta:
O (desde)
Pero ahora nuestro papel lo juega esta expresión:
Entonces podemos escribir:
¡Nuestro objetivo con usted es asegurarnos de que el lado izquierdo quede simple, sin “impurezas”!
¡Vamos a deshacernos de ellos poco a poco!
Primero, eliminemos el denominador en: para hacer esto, multipliquemos nuestra igualdad por:
Ahora eliminémoslo dividiendo ambas partes en él:
Ahora deshagámonos de los ocho:
La expresión resultante se puede escribir como 2 series de soluciones (por analogía con una ecuación cuadrática, donde sumamos o restamos el discriminante)
¡Necesitamos encontrar la raíz negativa más grande! Está claro que tenemos que solucionarlo.
Veamos primero el primer episodio:
Está claro que si tomamos, como resultado obtendremos números positivos, pero no nos interesan.
Entonces debes tomarlo como negativo. Permitir.
Cuando la raíz será más estrecha:
¡¡Y hay que encontrar el mayor negativo!! Esto significa que ir en dirección negativa ya no tiene sentido aquí. Y la raíz negativa más grande de esta serie será igual a.
Ahora veamos la segunda serie:
Y nuevamente sustituimos: , entonces:
¡No interesado!
¡Entonces no tiene sentido seguir aumentando! ¡Reducámoslo! Vamos entonces:
¡Encaja!
Permitir. Entonces
Entonces, ¡la raíz negativa más grande!
Respuesta:
Tarea número 2
Resolvemos nuevamente, independientemente del argumento del coseno complejo:
Ahora volvemos a expresar por la izquierda:
Multiplica ambos lados por
Dividir ambos lados por
Sólo queda moverlo hacia la derecha, cambiando su signo de menos a más.
Nuevamente obtenemos 2 series de raíces, una con y otra con.
Necesitamos encontrar la raíz negativa más grande. Veamos el primer episodio:
Está claro que obtendremos la primera raíz negativa en, será igual y será la raíz negativa más grande en 1 serie.
Para la segunda serie
La primera raíz negativa también se obtendrá en y será igual a. Desde entonces es la raíz negativa más grande de la ecuación.
Respuesta: .
Tarea número 3
Resolvemos, independientemente del argumento tangente complejo.
Ahora bien, no parece complicado, ¿verdad?
Como antes, expresamos en el lado izquierdo:
Bueno, eso es genial, ¡aquí solo hay una serie de raíces! Encontremos nuevamente el mayor negativo.
Está claro que resulta si lo dejas. Y esta raíz es igual.
Respuesta:
Ahora intente resolver usted mismo los siguientes problemas.
Tarea o 3 tareas para resolver de forma independiente.
- Resuelve la ecuación.
- Resuelve la ecuación.
En la respuesta a la raíz pi-shi-th-la-más pequeña posible. - Resuelve la ecuación.
En la respuesta a la raíz pi-shi-th-la-más pequeña posible.
¿Listo? Vamos a revisar. No describiré en detalle todo el algoritmo de solución; me parece que ya ha recibido suficiente atención anteriormente.
Bueno, ¿está todo bien? ¡Oh, esos desagradables senos nasales, siempre tienen algún tipo de problema!
Bueno, ¡ahora puedes resolver ecuaciones trigonométricas simples!
Consulte las soluciones y respuestas:
Tarea número 1
vamos a expresar
La raíz positiva más pequeña se obtiene si ponemos, ya que, entonces
Respuesta:
Tarea número 2
La raíz positiva más pequeña se obtiene en.
Será igual.
Respuesta: .
Tarea número 3
Cuando lo consigamos, cuando lo tengamos.
Respuesta: .
Este conocimiento le ayudará a resolver muchos problemas que encontrará en el examen.
Si está solicitando una calificación de “5”, entonces solo necesita continuar leyendo el artículo para nivel medio, que se dedicará a resolver ecuaciones trigonométricas más complejas (tarea C1).
NIVEL PROMEDIO
En este artículo describiré resolver ecuaciones trigonométricas más tipo complejo y cómo seleccionar sus raíces. Aquí me basaré en los siguientes temas:
- Ecuaciones trigonométricas para nivel principiante (ver arriba).
Las ecuaciones trigonométricas más complejas son la base para problemas avanzados. Requieren tanto resolver la ecuación en sí en forma general como encontrar las raíces de esta ecuación que pertenecen a un determinado intervalo dado.
Resolver ecuaciones trigonométricas se reduce a dos subtareas:
- Resolviendo la ecuación
- Selección de raíz
Cabe señalar que el segundo no siempre es necesario, pero en la mayoría de los ejemplos aún se requiere la selección. Pero si no es necesario, entonces podemos simpatizar con usted; esto significa que la ecuación es bastante compleja en sí misma.
Mi experiencia en el análisis de problemas C1 muestra que generalmente se dividen en las siguientes categorías.
Cuatro categorías de tareas de mayor complejidad (anteriormente C1)
- Ecuaciones que se reducen a factorización.
- Ecuaciones reducidas a la forma.
- Ecuaciones resueltas cambiando una variable.
- Ecuaciones que requieren selección adicional de raíces debido a irracionalidad o denominador.
En pocas palabras: si te atrapan una de las ecuaciones de los primeros tres tipos, entonces considérate afortunado. Para ellos, por regla general, también es necesario seleccionar raíces que pertenezcan a un intervalo determinado.
Si te encuentras con una ecuación del tipo 4, entonces tienes menos suerte: necesitas jugar con ella por más tiempo y con más cuidado, pero muy a menudo no requiere una selección adicional de raíces. No obstante, analizaré este tipo de ecuaciones en el próximo artículo, y este lo dedicaré a resolver ecuaciones de los tres primeros tipos.
Ecuaciones que se reducen a factorización.
Lo más importante que debes recordar para resolver este tipo de ecuación es
Como muestra la práctica, este conocimiento suele ser suficiente. Veamos algunos ejemplos:
Ejemplo 1. Ecuación reducida a factorización usando las fórmulas de reducción y seno de doble ángulo
- resolver la ecuacion
- Encuentra todas las raíces de esta ecuación que se encuentran por encima del corte.
Aquí, como prometí, las fórmulas de reducción funcionan:
Entonces mi ecuación se verá así:
Entonces mi ecuación tomará la siguiente forma:
Un estudiante miope podría decir: ¡ahora reduciré ambos lados, obtendré la ecuación más simple y disfrutaré de la vida! ¡Y se equivocará amargamente!
| RECUERDA: ¡NUNCA PUEDES REDUCIR AMBOS LADOS DE UNA ECUACIÓN TRIGONOMÉTRICA POR UNA FUNCIÓN QUE CONTIENE UNA DESCONOCIDA! ¡PARA QUE PIERDAS TUS RAÍCES! |
¿Entonces lo que hay que hacer? Sí, es sencillo, mueve todo a un lado y saca el factor común:
Bueno, lo factorizamos en factores, ¡hurra! Ahora decidamos:
La primera ecuación tiene raíces:
Y el segundo:
Esto completa la primera parte del problema. Ahora necesitas seleccionar las raíces:
La brecha es así:
O también se puede escribir así:
Bueno, vayamos a las raíces:
Primero, trabajemos con el primer episodio (¡y es más simple, por decir lo menos!)
Dado que nuestro intervalo es completamente negativo, no es necesario tomar intervalos no negativos, aún así darán raíces no negativas.
Entonces, tomémoslo: es demasiado, no acierta.
Entonces déjalo así, no volví a golpearlo.
Un intento más, luego, ¡sí, lo tengo! ¡Se ha encontrado la primera raíz!
Disparo de nuevo: ¡luego golpeo de nuevo!
Bueno, una vez más: : - esto ya es un vuelo.
Entonces de la primera serie hay 2 raíces que pertenecen al intervalo: .
Estamos trabajando con la segunda serie (estamos construyendo a la potencia según la regla):
¡No alcanzar!
¡Otra vez echándolo de menos!
¡Otra vez echándolo de menos!
¡Entiendo!
¡Vuelo!
Por tanto, mi intervalo tiene las siguientes raíces:
Este es el algoritmo que usaremos para resolver todos los demás ejemplos. Practiquemos juntos con un ejemplo más.
Ejemplo 2. Ecuación reducida a factorización mediante fórmulas de reducción
- Resuelve la ecuación
Solución:
De nuevo las famosas fórmulas de reducción:
¡No intentes recortar de nuevo!
La primera ecuación tiene raíces:
Y el segundo:
Ahora de nuevo la búsqueda de raíces.
Comenzaré con el segundo episodio, ¡ya sé todo por el ejemplo anterior! Mira y asegúrate de que las raíces pertenecientes al intervalo sean las siguientes:
Ahora el primer episodio y es más sencillo:
Si - adecuado
Si eso también está bien
Si ya es un vuelo.
Entonces las raíces quedarán de la siguiente manera:
Trabajo independiente. 3 ecuaciones.
Bueno, ¿te queda clara la técnica? ¿Resolver ecuaciones trigonométricas ya no parece tan difícil? Luego resuelva rápidamente los siguientes problemas usted mismo y luego resolveremos otros ejemplos:
- Resuelve la ecuación
Encuentra todas las raíces de esta ecuación que se encuentran por encima del intervalo. - resolver la ecuacion
Indique las raíces de la ecuación que se encuentran encima del corte. - resolver la ecuacion
Encuentra todas las raíces de esta ecuación que se encuentran entre ellas.
Ecuación 1.
Y nuevamente la fórmula de reducción:
Primera serie de raíces:
Segunda serie de raíces:
Comenzamos la selección para la brecha.
Respuesta: , .
Ecuación 2. Comprobación del trabajo independiente.
Una agrupación bastante complicada en factores (usaré la fórmula del seno del doble ángulo):
entonces o
Esta es una solución general. Ahora necesitamos seleccionar las raíces. El problema es que no podemos decir el valor exacto de un ángulo cuyo coseno es igual a un cuarto. Por lo tanto, no puedo simplemente deshacerme del arco coseno, ¡qué pena!
Lo que puedo hacer es darme cuenta de que sí, entonces.
Creemos una tabla: intervalo:
Bueno, a través de búsquedas dolorosas llegamos a la decepcionante conclusión de que nuestra ecuación tiene una raíz en el intervalo indicado: \displaystyle arccos\frac(1)(4)-5\pi
Ecuación 3: Prueba de trabajo independiente.
Una ecuación que parece aterradora. Sin embargo, se puede resolver de forma bastante sencilla aplicando la fórmula del seno del doble ángulo:
Reducámoslo a 2:
Agrupemos el primer término con el segundo y el tercero con el cuarto y saquemos los factores comunes:
Está claro que la primera ecuación no tiene raíces, y ahora consideremos la segunda:
En general, iba a detenerme un poco más tarde en resolver este tipo de ecuaciones, pero como apareció, no hay nada que hacer, tengo que resolver...
Ecuaciones de la forma:
Esta ecuación se resuelve dividiendo ambos lados por:
Por tanto, nuestra ecuación tiene una única serie de raíces:
Necesitamos encontrar aquellos que pertenecen al intervalo: .
Construyamos una tabla nuevamente, como hice antes:
Respuesta: .
Ecuaciones reducidas a la forma:
Bueno, ahora es el momento de pasar a la segunda parte de ecuaciones, especialmente porque ya he contado en qué consiste la solución de ecuaciones trigonométricas de un nuevo tipo. Pero vale la pena repetir que la ecuación es de la forma
Resuelto dividiendo ambos lados por coseno:
- resolver la ecuacion
Indique las raíces de la ecuación que se encuentran encima del corte. - resolver la ecuacion
Indique las raíces de la ecuación que se encuentran entre ellas.
Ejemplo 1.
El primero es bastante sencillo. Muévete hacia la derecha y aplica la fórmula del coseno de doble ángulo:
¡Sí! Ecuación de la forma: . Divido ambas partes por
Realizamos análisis de raíces:
Brecha:
Respuesta:
Ejemplo 2.
Todo también es bastante trivial: abramos los corchetes de la derecha:
Identidad trigonométrica básica:
Seno de doble ángulo:
Finalmente obtenemos:
Cribado de raíces: intervalo.
Respuesta: .
Bueno, ¿a ti te gusta la técnica, no es demasiado complicada? Espero que no. Inmediatamente podemos hacer una reserva: en su forma pura, las ecuaciones que se reducen inmediatamente a una ecuación para la tangente son bastante raras. Normalmente, esta transición (división por coseno) es sólo una parte de un problema más complejo. Aquí te dejamos un ejemplo para que practiques:
- resolver la ecuacion
- Encuentra todas las raíces de esta ecuación que se encuentran por encima del corte.
Vamos a revisar:
La ecuación se puede resolver inmediatamente; basta con dividir ambos lados por:
Detección de raíces:
Respuesta: .
De una forma u otra, todavía tenemos que encontrar ecuaciones del tipo que acabamos de examinar. Sin embargo, es demasiado pronto para dar por terminado el día: todavía hay una “capa” más de ecuaciones que no hemos analizado. Entonces:
Resolver ecuaciones trigonométricas cambiando variables.
Aquí todo es transparente: miramos de cerca la ecuación, la simplificamos tanto como sea posible, hacemos una sustitución, la resolvemos, ¡hacemos una sustitución inversa! En palabras todo es muy fácil. Veámoslo en acción:
Ejemplo.
- Resuelve la ecuación: .
- Encuentra todas las raíces de esta ecuación que se encuentran por encima del corte.
Bueno, ¡aquí se nos sugiere el reemplazo!
Entonces nuestra ecuación se convertirá en esto:
La primera ecuación tiene raíces:
Y el segundo es así:
Ahora encontremos las raíces pertenecientes al intervalo.
Respuesta: .
Veamos juntos un ejemplo un poco más complejo:
- resolver la ecuacion
- Indique las raíces de la ecuación dada, que se encuentran arriba y entre ellas.
Aquí el reemplazo no es visible de inmediato, además, no es muy obvio. Pensemos primero: ¿qué podemos hacer?
Podemos, por ejemplo, imaginar
Y al mismo tiempo
Entonces mi ecuación tomará la forma:
Y ahora atención, concéntrate:
Dividamos ambos lados de la ecuación por:
¡De repente tú y yo tenemos una ecuación cuadrática relativa! Hagamos un reemplazo, luego obtenemos:
La ecuación tiene las siguientes raíces:
Segunda serie de raíces desagradables, ¡pero no se puede hacer nada! Seleccionamos raíces en el intervalo.
También debemos considerar que
Desde y entonces
Respuesta:
Para reforzar esto antes de que resuelvas los problemas tú mismo, aquí tienes otro ejercicio:
- resolver la ecuacion
- Encuentra todas las raíces de esta ecuación que se encuentran entre ellas.
Aquí debes mantener los ojos abiertos: ¡ahora tenemos denominadores que pueden ser cero! ¡Por lo tanto, debes estar especialmente atento a las raíces!
En primer lugar, necesito reorganizar la ecuación para poder hacer una sustitución adecuada. No se me ocurre nada mejor ahora que reescribir la tangente en términos de seno y coseno:
Ahora pasaré del coseno al seno usando la identidad trigonométrica básica:
Y finalmente, llevaré todo a un denominador común:
Ahora puedo pasar a la ecuación:
Pero en (es decir, en).
Ahora todo está listo para ser reemplazado:
Entonces o
Sin embargo, tenga en cuenta que si, ¡al mismo tiempo!
¿Quién sufre esto? El problema de la tangente es que no está definida cuando el coseno es igual a cero (se produce la división por cero).
Así, las raíces de la ecuación son:
Ahora tamizamos las raíces en el intervalo:
| - encaja | |
| - exagerar |
Por tanto, nuestra ecuación tiene una raíz única en el intervalo y es igual.
Verás: la aparición de un denominador (¡al igual que la tangente, conlleva ciertas dificultades con las raíces! ¡Aquí hay que tener más cuidado!).
Bueno, tú y yo casi hemos terminado de analizar ecuaciones trigonométricas, queda muy poco para resolver dos problemas por tu cuenta. Aquí están.
- Resuelve la ecuación
Encuentra todas las raíces de esta ecuación que se encuentran por encima del corte. - resolver la ecuacion
Indique las raíces de esta ecuación, ubicadas encima del corte.
¿Decidido? ¿No es muy difícil? Vamos a revisar:
- Trabajamos según las fórmulas de reducción:
Sustituye en la ecuación:
Reescribamos todo mediante cosenos para que sea más fácil realizar el reemplazo:
Ahora es fácil hacer un reemplazo:
Está claro que es una raíz extraña, ya que la ecuación no tiene soluciones. Entonces:
Buscamos las raíces que necesitamos en el intervalo.
Respuesta: .
Aquí el reemplazo es inmediatamente visible:Entonces o
- ¡encaja! - ¡encaja! - ¡encaja! - ¡encaja! - ¡mucho! - ¡también mucho! Respuesta:
Bueno, ¡eso es todo ahora! Pero la resolución de ecuaciones trigonométricas no termina ahí; nos quedamos atrás en los casos más difíciles: cuando las ecuaciones contienen irracionalidad o varios tipos de “denominadores complejos”. Veremos cómo resolver este tipo de tareas en un artículo para un nivel avanzado.
NIVEL AVANZADO
Además de las ecuaciones trigonométricas analizadas en los dos artículos anteriores, consideraremos otra clase de ecuaciones que requieren un análisis aún más cuidadoso. Estos ejemplos trigonométricos contienen irracionalidad o un denominador, lo que dificulta su análisis.. Sin embargo, es posible que encuentre estas ecuaciones en la Parte C del examen. Sin embargo, cada nube tiene un lado positivo: para tales ecuaciones, por regla general, ya no se plantea la cuestión de cuál de sus raíces pertenece a un intervalo dado. No nos andemos con rodeos, sino que vayamos directamente a los ejemplos trigonométricos.
Ejemplo 1.
Resuelve la ecuación y encuentra las raíces que pertenecen al segmento.
Solución:
¡Tenemos un denominador que no debería ser igual a cero! Entonces resolver esta ecuación es lo mismo que resolver el sistema
Resolvamos cada una de las ecuaciones:
Y ahora el segundo:
Ahora veamos la serie:
Está claro que esta opción no nos conviene, ya que en este caso nuestro denominador se pone a cero (ver la fórmula de las raíces de la segunda ecuación)
Si es así, ¡todo está en orden y el denominador no es cero! Entonces las raíces de la ecuación son las siguientes: , .
Ahora seleccionamos las raíces pertenecientes al intervalo.
| - no adecuado | - encaja | |
| - encaja | - encaja | |
| exagerar | exagerar |
Entonces las raíces son las siguientes:
Verá, incluso la aparición de una pequeña alteración en la forma del denominador afectó significativamente la solución de la ecuación: descartamos una serie de raíces que anulaban el denominador. Las cosas pueden complicarse aún más si te encuentras con ejemplos trigonométricos que son irracionales.
Ejemplo 2.
Resuelve la ecuación:
Solución:
Bueno, al menos no hay que quitarle las raíces, ¡y eso es bueno! Primero resolvamos la ecuación, independientemente de la irracionalidad:
Entonces, ¿eso es todo? ¡No, ay, sería demasiado fácil! Debemos recordar que bajo la raíz sólo pueden aparecer números no negativos. Entonces:
La solución a esta desigualdad es:
Ahora queda por descubrir si parte de las raíces de la primera ecuación terminaron inadvertidamente donde la desigualdad no se cumple.
Para hacer esto, puedes usar nuevamente la tabla:
| : , Pero | ¡No! | |
| ¡Sí! | ||
| ¡Sí! |
¡Así, una de mis raíces “se cayó”! Resulta si lo dejas. Entonces la respuesta se puede escribir de la siguiente manera:
Respuesta:
Verás, ¡la raíz requiere aún más atención! Hagámoslo más complicado: ahora tengo una función trigonométrica debajo de mi raíz.
Ejemplo 3.
Como antes: primero resolveremos cada uno por separado, y luego pensaremos en lo que hemos hecho.
Ahora la segunda ecuación:
Ahora lo más difícil es saber si se obtienen valores negativos bajo la raíz aritmética si sustituimos allí las raíces de la primera ecuación:
El número debe entenderse en radianes. Dado que un radianes equivale aproximadamente a grados, los radianes son del orden de grados. Esta es la esquina del segundo cuarto. ¿Cuál es el signo del coseno del segundo cuarto? Menos. ¿Qué pasa con el seno? Más. Entonces, ¿qué podemos decir sobre la expresión?
¡Es menos que cero!
Esto significa que no es la raíz de la ecuación.
Ahora es el momento.
Comparemos este número con cero.
La cotangente es una función que decrece en 1 trimestre (cuanto menor es el argumento, mayor es la cotangente). los radianes son aproximadamente grados. Al mismo tiempo
desde entonces y por lo tanto
,
Respuesta: .
¿Podría volverse más complicado? ¡Por favor! Será más difícil si la raíz sigue siendo una función trigonométrica y la segunda parte de la ecuación vuelve a ser una función trigonométrica.
Cuantos más ejemplos trigonométricos, mejor, consulte a continuación:
Ejemplo 4.
La raíz no es adecuada debido al coseno limitado.
Ahora el segundo:
Al mismo tiempo, por definición de raíz:
Debemos recordar el círculo unitario: es decir, aquellos cuartos donde el seno es menor que cero. ¿Cuáles son estos cuartos? Tercero y cuarto. Entonces nos interesarán aquellas soluciones de la primera ecuación que se encuentran en el tercer o cuarto trimestre.
La primera serie da raíces que se encuentran en la intersección del tercer y cuarto cuarto. La segunda serie, diametralmente opuesta a ella, da lugar a raíces que se encuentran en el borde del primer y segundo cuarto. Por tanto, esta serie no es adecuada para nosotros.
Respuesta: ,
Y otra vez Ejemplos trigonométricos con "irracionalidad difícil". ¡No solo tenemos nuevamente la función trigonométrica debajo de la raíz, sino que ahora también está en el denominador!
Ejemplo 5.
Bueno, no se puede hacer nada, hacemos lo mismo que antes.
Ahora trabajamos con el denominador:
No quiero resolver la desigualdad trigonométrica, así que haré algo inteligente: tomaré y sustituiré mi serie de raíces en la desigualdad:
Si - es par, entonces tenemos:
ya que todos los ángulos de visión se encuentran en el cuarto trimestre. Y de nuevo la sagrada pregunta: ¿cuál es el signo del seno en el cuarto cuarto? Negativo. Entonces la desigualdad
Si es impar, entonces:
¿En qué cuarto se encuentra el ángulo? Esta es la esquina del segundo cuarto. Entonces todas las esquinas vuelven a ser las esquinas del segundo cuarto. El seno allí es positivo. ¡Justo lo que necesitas! Entonces la serie:
¡Encaja!
Tratamos la segunda serie de raíces de la misma manera:
Sustituimos en nuestra desigualdad:
Si - incluso, entonces
Córners del primer cuarto. El seno allí es positivo, lo que significa que la serie es adecuada. Ahora bien, si es impar, entonces:
¡También encaja!
Bueno, ¡ahora anotamos la respuesta!
Respuesta:
Bueno, este fue quizás el caso que requirió más mano de obra. Ahora te ofrezco problemas para que los resuelvas por tu cuenta.
Capacitación
- Resuelve y encuentra todas las raíces de la ecuación que pertenecen al segmento.
Soluciones:
Primera ecuación:
o
ODZ raíz:Segunda ecuación:
Selección de raíces que pertenecen al intervalo.
Respuesta:
O
o
Pero
Consideremos: . Si - incluso, entonces
- ¡no encaja!
Si es impar: ¡adecuado!
Esto significa que nuestra ecuación tiene la siguiente serie de raíces:
o
Selección de raíces en el intervalo:
| - no adecuado | - encaja | |
| - encaja | - mucho | |
| - encaja | mucho |
Respuesta: , .
O
Desde entonces la tangente no está definida. ¡Descartamos inmediatamente esta serie de raíces!
Segunda parte:
Al mismo tiempo, según DZ se requiere que
Comprobamos las raíces encontradas en la primera ecuación:
Si el signo:
Ángulos del primer cuarto donde la tangente es positiva. ¡No encaja!
Si el signo:
Esquina del cuarto cuarto. Allí la tangente es negativa. Encaja. Anotamos la respuesta:
Respuesta: , .
Hemos analizado juntos ejemplos trigonométricos complejos en este artículo, pero debes resolver las ecuaciones tú mismo.
RESUMEN Y FÓRMULAS BÁSICAS
Una ecuación trigonométrica es una ecuación en la que la incógnita está estrictamente bajo el signo de la función trigonométrica.
Hay dos formas de resolver ecuaciones trigonométricas:
La primera forma es utilizar fórmulas.
La segunda forma es a través del círculo trigonométrico.
Le permite medir ángulos, encontrar sus senos, cosenos, etc.
¡¡¡Puede solicitar una solución detallada a su problema!!!
Una igualdad que contiene una incógnita bajo el signo de una función trigonométrica (`sin x, cos x, tan x` o `ctg x`) se llama ecuación trigonométrica, y son sus fórmulas las que consideraremos más a fondo.
Las ecuaciones más simples son `sin x=a, cos x=a, tg x=a, ctg x=a`, donde `x` es el ángulo que se va a encontrar, `a` es cualquier número. Anotemos las fórmulas raíz de cada uno de ellos.
1. Ecuación `sen x=a`.
Para `|a|>1` no tiene soluciones.
Cuando `|a| \leq 1` tiene un número infinito de soluciones.
Fórmula raíz: `x=(-1)^n arcsin a + \pi n, n \in Z`
2. Ecuación `cos x=a`
Para `|a|>1` - como en el caso del seno, no tiene soluciones entre los números reales.
Cuando `|a| \leq 1` tiene un número infinito de soluciones.
Fórmula raíz: `x=\pm arccos a + 2\pi n, n \in Z`

Casos especiales de seno y coseno en gráficas. 
3. Ecuación `tg x=a`
Tiene un número infinito de soluciones para cualquier valor de "a".
Fórmula raíz: `x=arctg a + \pi n, n \in Z`

4. Ecuación `ctg x=a`
También tiene un número infinito de soluciones para cualquier valor de "a".
Fórmula raíz: `x=arcctg a + \pi n, n \in Z`

Fórmulas para las raíces de ecuaciones trigonométricas en la tabla.
Para seno:  Para coseno:
Para coseno:  Para tangente y cotangente:
Para tangente y cotangente:  Fórmulas para resolver ecuaciones que contienen funciones trigonométricas inversas:
Fórmulas para resolver ecuaciones que contienen funciones trigonométricas inversas:

Métodos para resolver ecuaciones trigonométricas.
Resolver cualquier ecuación trigonométrica consta de dos etapas:
- con la ayuda de transformarlo al más simple;
- resuelva la ecuación más simple obtenida usando las fórmulas de raíz y las tablas escritas arriba.
Veamos los principales métodos de solución mediante ejemplos.
Método algebraico.
Este método implica reemplazar una variable y sustituirla en una igualdad.
Ejemplo. Resuelve la ecuación: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 - x)+1=0`
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
haga un reemplazo: `cos(x+\frac \pi 6)=y`, luego `2y^2-3y+1=0`,
encontramos las raíces: `y_1=1, y_2=1/2`, de lo que se siguen dos casos:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3- \frac \pi 6+2\pi n`.
Respuesta: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Factorización.
Ejemplo. Resuelve la ecuación: `sen x+cos x=1`.
Solución. Movamos todos los términos de la igualdad hacia la izquierda: `sin x+cos x-1=0`. Usando , transformamos y factorizamos el lado izquierdo:
`pecado x — 2pecado^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sen x/2 (cos x/2-sen x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sen x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n` , `x_2=\pi/2+ 2\pi n`.
Respuesta: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Reducción a una ecuación homogénea
Primero, necesitas reducir esta ecuación trigonométrica a una de dos formas:
`a sin x+b cos x=0` (ecuación homogénea de primer grado) o `a sin^2 x + b sin x cos x +c cos^2 x=0` (ecuación homogénea de segundo grado).
Luego divida ambas partes por `cos x \ne 0` - para el primer caso, y por `cos^2 x \ne 0` - para el segundo. Obtenemos ecuaciones para `tg x`: `a tg x+b=0` y `a tg^2 x + b tg x +c =0`, que deben resolverse utilizando métodos conocidos.
Ejemplo. Resuelve la ecuación: `2 sin^2 x+sin x cos x - cos^2 x=1`.
Solución. Escribamos el lado derecho como `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`pecado^2 x+pecado x cos x — 2 cos^2 x=0`.
Esta es una ecuación trigonométrica homogénea de segundo grado, dividimos sus lados izquierdo y derecho por `cos^2 x \ne 0`, obtenemos:
`\frac (sin^2 x)(cos^2 x)+\frac(sin x cos x)(cos^2 x) — \frac(2 cos^2 x)(cos^2 x)=0`
`tg^2x+tgx — 2=0`. Introduzcamos el reemplazo `tg x=t`, lo que resulta en `t^2 + t - 2=0`. Las raíces de esta ecuación son `t_1=-2` y `t_2=1`. Entonces:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.
Respuesta. `x_1=arctg (-2)+\pi n`, `n \en Z`, `x_2=\pi/4+\pi n`, `n \en Z`.
Moviéndose a medio ángulo
Ejemplo. Resuelve la ecuación: `11 sen x - 2 cos x = 10`.
Solución. Apliquemos las fórmulas de los ángulos dobles, lo que da como resultado: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x /2 +10 cos^2 x/2`
`4 tg^2 x/2 — 11 tgx/2 +6=0`
Aplicando el método algebraico descrito anteriormente, obtenemos:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Respuesta. `x_1=2 arctg 2+2\pi n, n \en Z`, `x_2=arctg 3/4+2\pi n`, `n \en Z`.
Introducción del ángulo auxiliar.
En la ecuación trigonométrica `a sin x + b cos x =c`, donde a,b,c son coeficientes y x es una variable, divide ambos lados por `sqrt (a^2+b^2)`:
`\frac a(sqrt (a^2+b^2)) sin x +` `\frac b(sqrt (a^2+b^2)) cos x =` `\frac c(sqrt (a^2) ) +b^2))`.
Los coeficientes del lado izquierdo tienen las propiedades del seno y el coseno, es decir, la suma de sus cuadrados es igual a 1 y sus módulos no son mayores que 1. Denotémoslos de la siguiente manera: `\frac a(sqrt (a^2 +b^2))=cos \varphi` , ` \frac b(sqrt (a^2+b^2)) =sin \varphi`, `\frac c(sqrt (a^2+b^2)) =C`, entonces:
`cos \varphi sin x + sin \varphi cos x =C`.
Echemos un vistazo más de cerca al siguiente ejemplo:
Ejemplo. Resuelve la ecuación: `3 sen x+4 cos x=2`.
Solución. Dividiendo ambos lados de la igualdad por `sqrt (3^2+4^2)`, obtenemos:
`\frac (3 sin x) (sqrt (3^2+4^2))+` `\frac(4 cos x)(sqrt (3^2+4^2))=` `\frac 2(sqrt (3^2+4^2))`
`3/5 sen x+4/5 porque x=2/5`.
Denotemos `3/5 = cos \varphi`, `4/5=sin \varphi`. Dado que `sin \varphi>0`, `cos \varphi>0`, entonces tomamos `\varphi=arcsin 4/5` como ángulo auxiliar. Luego escribimos nuestra igualdad en la forma:
`cos \varphi sin x+sin \varphi cos x=2/5`
Aplicando la fórmula para la suma de ángulos del seno, escribimos nuestra igualdad de la siguiente forma:
`pecado (x+\varphi)=2/5`,
`x+\varphi=(-1)^n arcosen 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcosin 2/5-` `arcossin 4/5+ \pi n`, `n \in Z`.
Respuesta. `x=(-1)^n arcosin 2/5-` `arcossin 4/5+ \pi n`, `n \in Z`.
Ecuaciones trigonométricas racionales fraccionarias
Se trata de igualdades con fracciones cuyos numeradores y denominadores contienen funciones trigonométricas.
Ejemplo. Resuelve la ecuación. `\frac (sin x)(1+cos x)=1-cos x`.
Solución. Multiplica y divide el lado derecho de la igualdad por `(1+cos x)`. Como resultado obtenemos:
`\frac (sin x)(1+cos x)=` `\frac ((1-cos x)(1+cos x))(1+cos x)`
`\frac (sin x)(1+cos x)=` `\frac (1-cos^2 x)(1+cos x)`
`\frac (sin^2 x)(1+cos x)=` `\frac (sin^2 x)(1+cos x)`
`\frac (sin^2 x)(1+cos x)-` `\frac (sin^2 x)(1+cos x)=0`
`\frac (sin x-sin^2 x)(1+cos x)=0`
Considerando que el denominador no puede ser igual a cero, obtenemos `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Igualemos el numerador de la fracción a cero: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Entonces `sin x=0` o `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \en Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Dado que ` x \ne \pi+2\pi n, n \in Z`, las soluciones son `x=2\pi n, n \in Z` y `x=\pi /2+2\pi n` , `n\en Z`.
Respuesta. `x=2\pi n`, `n \en Z`, `x=\pi /2+2\pi n`, `n \en Z`.
La trigonometría, y las ecuaciones trigonométricas en particular, se utilizan en casi todas las áreas de la geometría, la física y la ingeniería. Los estudios comienzan en el décimo grado, siempre hay tareas para el Examen Estatal Unificado, así que trate de recordar todas las fórmulas de ecuaciones trigonométricas: ¡definitivamente le serán útiles!
Sin embargo, ni siquiera es necesario memorizarlos, lo principal es comprender la esencia y poder deducirla. No es tan difícil como parece. Compruébalo tú mismo viendo el vídeo.
Las ecuaciones trigonométricas más simples son las ecuaciones.
Cos (x) = a, sen (x) = a, tg (x) = a, ctg (x) =a
Ecuación cos(x) = a

Explicación y fundamento
- Las raíces de la ecuación cosx = a. Cuando | un | > 1 la ecuación no tiene raíces, ya que | cosx |< 1 для любого x (прямая y = а при а >1 o en un< -1 не пересекает график функцииy = cosx).
Deja | un |< 1. Тогда прямая у = а пересекает график функции
y = cos x. En el intervalo, la función y = cos x disminuye de 1 a -1. Pero una función decreciente toma cada uno de sus valores solo en un punto de su dominio de definición, por lo tanto la ecuación cos x = a tiene solo una raíz en este intervalo, que, por definición de arcocoseno, es igual a: x 1 = arccos a (y para esta raíz cos x = A).
El coseno es una función par, por lo que en el intervalo [-n; 0] la ecuación cos x = y también tiene una sola raíz: el número opuesto a x 1, es decir
x 2 = -arcos a.
Así, en el intervalo [-n; p] (longitud 2p) ecuación cos x = a con | un |< 1 имеет только корни x = ±arccos а.
La función y = cos x es periódica con un período de 2n, por lo tanto todas las demás raíces difieren de las encontradas por 2n (n € Z). Obtenemos la siguiente fórmula para las raíces de la ecuación cos x = a cuando
x = ±arccos a + 2pp, n £ Z.
- Casos especiales de resolución de la ecuación cosx = a.
Es útil recordar notaciones especiales para las raíces de la ecuación cos x = a cuando
a = 0, a = -1, a = 1, que se puede obtener fácilmente usando el círculo unitario como referencia.
Como el coseno es igual a la abscisa del punto correspondiente del círculo unitario, obtenemos que cos x = 0 si y sólo si el punto correspondiente del círculo unitario es el punto A o el punto B.
De manera similar, cos x = 1 si y solo si el punto correspondiente del círculo unitario es el punto C, por lo tanto,
x = 2πп, k€Z.
También cos x = -1 si y sólo si el punto correspondiente del círculo unitario es el punto D, por lo tanto x = n + 2n,



Ecuación sin(x) = a


Explicación y fundamento
- Las raíces de la ecuación sinx = a. Cuando | un | > 1 la ecuación no tiene raíces, ya que | pecado |< 1 для любого x (прямая y = а на рисунке при а >1 o en un< -1 не пересекает график функции y = sinx).
En esta lección veremos Funciones trigonométricas básicas, sus propiedades y gráficas., y también enumerar tipos básicos de ecuaciones y sistemas trigonométricos. Además, indicamos soluciones generales de las ecuaciones trigonométricas más simples y sus casos especiales.
Esta lección le ayudará a prepararse para uno de los tipos de tareas. B5 y C1.
Preparación para el Examen Estatal Unificado de Matemáticas.
Experimento
Lección 10. Funciones trigonométricas. Ecuaciones trigonométricas y sus sistemas.
Teoría
Resumen de la lección
Ya hemos utilizado muchas veces el término “función trigonométrica”. En la primera lección de este tema, los identificamos usando triángulo rectángulo y el círculo trigonométrico unitario. Usando estos métodos para especificar funciones trigonométricas, ya podemos concluir que para ellos un valor del argumento (o ángulo) corresponde exactamente a un valor de la función, es decir tenemos derecho a llamar funciones seno, coseno, tangente y cotangente.
En esta lección, es hora de intentar abstraerse de los métodos discutidos anteriormente para calcular los valores de funciones trigonométricas. Hoy pasaremos al enfoque algebraico habitual para trabajar con funciones, veremos sus propiedades y representaremos gráficas.
En cuanto a las propiedades de las funciones trigonométricas, se debe prestar especial atención a:
El dominio de la definición y el rango de valores, porque para seno y coseno existen restricciones en el rango de valores, y para tangente y cotangente hay restricciones en el rango de definición;
La periodicidad de todas las funciones trigonométricas, porque Ya hemos notado la presencia del argumento más pequeño distinto de cero, cuya suma no cambia el valor de la función. Este argumento se llama período de la función y se denota con la letra. Para seno/coseno y tangente/cotangente estos períodos son diferentes.
Considere la función:
1) Alcance de la definición;
2) rango de valores ![]() ;
;
3) La función es impar ![]() ;
;
Construyamos una gráfica de la función. En este caso, conviene comenzar la construcción con una imagen del área que limita la gráfica desde arriba con el número 1 y desde abajo con el número , que está asociado al rango de valores de la función. Además, para la construcción es útil recordar los valores de los senos de varios ángulos principales de la tabla, por ejemplo, que esto le permitirá construir la primera "onda" completa del gráfico y luego volver a dibujarla hacia la derecha y izquierda, aprovechando que la imagen se repetirá con un desplazamiento de un punto, es decir en .

Ahora veamos la función:
Las principales propiedades de esta función:
1) Alcance de la definición;
2) rango de valores ![]() ;
;
3) Función uniforme ![]() Esto implica que la gráfica de la función es simétrica con respecto a la ordenada;
Esto implica que la gráfica de la función es simétrica con respecto a la ordenada;
4) La función no es monótona en todo su dominio de definición;
Construyamos una gráfica de la función. Al igual que cuando se construye un seno, es conveniente comenzar con una imagen del área que limita la gráfica en la parte superior con el número 1 y en la parte inferior con el número , que está asociado al rango de valores de la función. También trazaremos las coordenadas de varios puntos en el gráfico, para lo cual debemos recordar los valores de los cosenos de varios ángulos principales de la tabla, por ejemplo, que con la ayuda de estos puntos podemos construir la primera "onda" completa. ” del gráfico y luego volver a dibujarlo hacia la derecha y hacia la izquierda, aprovechando que la imagen se repetirá con un cambio de período, es decir en .

Pasemos a la función:
Las principales propiedades de esta función:
1) Dominio excepto , donde . Ya hemos indicado en lecciones anteriores que no existe. Esta afirmación se puede generalizar considerando el período tangente;
2) Rango de valores, es decir los valores tangentes no están limitados;
3) La función es impar ![]() ;
;
4) La función aumenta monótonamente dentro de sus denominadas ramas tangentes, que ahora veremos en la figura;
5) La función es periódica con un punto.
Construyamos una gráfica de la función. En este caso, es conveniente comenzar la construcción representando las asíntotas verticales del gráfico en puntos que no están incluidos en el dominio de definición, es decir, etc. A continuación, representamos las ramas de la tangente dentro de cada una de las franjas formadas por las asíntotas, presionándolas hacia la asíntota izquierda y hacia la derecha. Al mismo tiempo, no olvides que cada rama aumenta de forma monótona. Representamos todas las ramas de la misma manera, porque la función tiene un periodo igual a . Esto se puede ver en el hecho de que cada rama se obtiene desplazando la vecina a lo largo del eje de abscisas.

Y terminamos con un vistazo a la función:
Las principales propiedades de esta función:
1) Dominio excepto , donde . Por la tabla de valores de funciones trigonométricas ya sabemos que no existe. Esta afirmación se puede generalizar considerando el período cotangente;
2) Rango de valores, es decir los valores cotangentes no están limitados;
3) La función es impar ![]() ;
;
4) La función decrece monótonamente dentro de sus ramas, que son similares a las ramas tangentes;
5) La función es periódica con un punto.
Construyamos una gráfica de la función. En este caso, en cuanto a la tangente, es conveniente comenzar la construcción representando las asíntotas verticales del gráfico en puntos que no están incluidos en el área de definición, es decir etc. A continuación, representamos las ramas de la cotangente dentro de cada una de las franjas formadas por las asíntotas, presionándolas hacia la asíntota izquierda y hacia la derecha. En este caso, tenemos en cuenta que cada rama disminuye de forma monótona. Representamos todas las ramas de manera similar a la tangente de la misma manera, porque la función tiene un periodo igual a .

Por otra parte, cabe señalar que las funciones trigonométricas con argumentos complejos pueden tener un período no estándar. Estamos hablando de funciones de la forma:
![]()
![]()
Su período es igual. Y sobre las funciones:
![]()
![]()
Su período es igual.
Como puede ver, para calcular un nuevo período, el período estándar simplemente se divide por el factor del argumento. No depende de otras modificaciones de la función.
Puede comprender con más detalle y comprender de dónde provienen estas fórmulas en la lección sobre la construcción y transformación de gráficas de funciones.
Hemos llegado a una de las partes más importantes del tema “Trigonometría”, que dedicaremos a la resolución de ecuaciones trigonométricas. La capacidad de resolver este tipo de ecuaciones es importante, por ejemplo, a la hora de describir procesos oscilatorios en física. Imaginemos que has dado algunas vueltas en un kart de un coche deportivo; resolver una ecuación trigonométrica te ayudará a determinar cuánto tiempo llevas corriendo en función de la posición del coche en la pista.
Escribamos la ecuación trigonométrica más simple:
La solución a tal ecuación son los argumentos cuyo seno es igual a . Pero ya sabemos que debido a la periodicidad del seno, existe un número infinito de tales argumentos. Por tanto, la solución a esta ecuación será, etc. Lo mismo se aplica a la resolución de cualquier otra ecuación trigonométrica simple; habrá un número infinito de ellas.
Las ecuaciones trigonométricas se dividen en varios tipos principales. Por separado, deberíamos detenernos en los más simples, porque todo lo demás depende de ellos. Hay cuatro ecuaciones de este tipo (según el número de funciones trigonométricas básicas). Se conocen soluciones generales para ellos; hay que recordarlas.
Las ecuaciones trigonométricas más simples y sus soluciones generales. se parece a esto:
Tenga en cuenta que los valores de seno y coseno deben tener en cuenta las limitaciones que conocemos. Si, por ejemplo, la ecuación no tiene soluciones y no se debe aplicar la fórmula especificada.
Además, las fórmulas raíz especificadas contienen un parámetro en forma de un número entero arbitrario. EN currículum escolar Este es el único caso en el que la solución de una ecuación sin parámetro contiene un parámetro. Este número entero arbitrario muestra que es posible escribir un número infinito de raíces de cualquiera de las ecuaciones anteriores simplemente sustituyendo todos los números enteros por turno.
Puede familiarizarse con la derivación detallada de estas fórmulas repitiendo el capítulo "Ecuaciones trigonométricas" en el programa de álgebra de décimo grado.
Por otra parte, es necesario prestar atención a la resolución de casos especiales de las ecuaciones más simples con seno y coseno. Estas ecuaciones se ven así:
No se les deben aplicar fórmulas para encontrar soluciones generales. La forma más conveniente de resolver estas ecuaciones es utilizando el círculo trigonométrico, que da un resultado más sencillo que las fórmulas de solución generales.
Por ejemplo, la solución de la ecuación es ![]() . Intenta obtener esta respuesta tú mismo y resuelve las ecuaciones restantes indicadas.
. Intenta obtener esta respuesta tú mismo y resuelve las ecuaciones restantes indicadas.
Además del tipo más común de ecuaciones trigonométricas indicadas, existen varias más estándar. Te los enumeramos teniendo en cuenta los que ya te hemos indicado:
1) Protozoos, Por ejemplo, ;
2) Casos especiales de las ecuaciones más simples., Por ejemplo, ;
3) Ecuaciones con argumento complejo, Por ejemplo, ![]() ;
;
4) Ecuaciones reducidas a su forma más simple quitando un factor común, Por ejemplo, ;
5) Ecuaciones reducidas a su forma más simple transformando funciones trigonométricas., Por ejemplo, ;
6) Ecuaciones reducidas a su forma más simple por sustitución, Por ejemplo, ;
7) Ecuaciones homogéneas, Por ejemplo, ;
8) Ecuaciones que se pueden resolver usando las propiedades de las funciones., Por ejemplo, ![]() . No se alarme por el hecho de que hay dos variables en esta ecuación; se resuelve sola;
. No se alarme por el hecho de que hay dos variables en esta ecuación; se resuelve sola;
Así como ecuaciones que se resuelven mediante diversos métodos.
Además de resolver ecuaciones trigonométricas, debes poder resolver sus sistemas.
Los tipos de sistemas más comunes son:
1) ¿En cuál de las ecuaciones es potencia?, Por ejemplo, ![]() ;
;
2) Sistemas de ecuaciones trigonométricas simples., Por ejemplo, ![]() .
.
En la lección de hoy analizamos las funciones trigonométricas básicas, sus propiedades y gráficas. También nos conocimos fórmulas generales Las soluciones de las ecuaciones trigonométricas más simples indicaron los principales tipos de tales ecuaciones y sus sistemas.
En la parte práctica de la lección, examinaremos métodos para resolver ecuaciones trigonométricas y sus sistemas.
Cuadro 1.Resolver casos especiales de las ecuaciones trigonométricas más simples..
Como ya hemos dicho en la parte principal de la lección, casos especiales de ecuaciones trigonométricas con seno y coseno de la forma:
tienen soluciones más simples que las dadas por las fórmulas de solución generales.
Para ello se utiliza un círculo trigonométrico. Analicemos el método para resolverlos usando el ejemplo de la ecuación.
Representaremos en el círculo trigonométrico el punto en el que el valor del coseno es cero, que también es la coordenada a lo largo del eje de abscisas. Como puede ver, hay dos de esos puntos. Nuestra tarea es indicar a qué es igual el ángulo que corresponde a estos puntos del círculo.
 |
Comenzamos a contar desde la dirección positiva del eje de abscisas (eje coseno) y al establecer el ángulo llegamos al primer punto representado, es decir. una solución sería este valor de ángulo. Pero todavía estamos satisfechos con el ángulo que corresponde al segundo punto. ¿Cómo entrar en ello?