Size: px
Start showing from the page:
Transcript
1 9th grade 1. Minimum path A car traveling at a speed υ at some moment begins to move with such constant acceleration that during the time τ the distance s traveled by it turns out to be minimal. Define this path s. 2. Reflection in flight In a ballistic laboratory, when conducting an experiment to study elastic reflection from moving obstacles u, a small ball was fired from a small catapult υ mounted on a horizontal surface. At the same time, from the point at which, according to calculations, the ball should have fallen, a massive vertical wall began to move towards it at a constant speed (see figure). After elastic reflection from the wall, the ball fell at some distance from the catapult. Then the experiment was repeated, changing only the speed of the wall. It turned out that in two experiments the ball hit the wall at the same height h. Determine this height if it is known that the time of flight of the ball before reflection in the first case was t1 = 1 s, and in the second case t2 = 2 s. To what maximum height H did the ball rise during the entire flight? What is the initial speed of the ball υ, if the distance between the places of its fall on the horizontal surface in the first and second experiments was L = 9 m? Define speeds uniform motion walls u1 and u2 in these experiments and the initial distance S between the wall and the catapult. Consider g = 1 m/s 2. Note. In the reference frame associated with the wall, the velocity modules of the ball before and after the collision are the same, and the angle of reflection of the ball is equal to the angle of incidence. 3. Three-cylinder A body glued together from three coaxial cylinders of different cross sections and different heights is immersed in some liquid and the dependence of the Archimedes force F acting on the body on the depth h of its immersion is removed. It is known that the cross-sectional area of the narrowest (not the fact that the lowest) cylinder is S = 1 cm 2. Plot a graph of F(h) and use it to determine the height of each of the cylinders, the cross-sectional areas of the other two cylinders and the density of the liquid. During the experiment, the axis of rotation of the cylinders remained vertical, g = 1 m/s 2. h, cm F a, H, 3.9 1.8 2.4 3.6 4.2 4.8 6, 7.2 7, 3 7.5 7.6 7.7 7.8 7.9 7.9
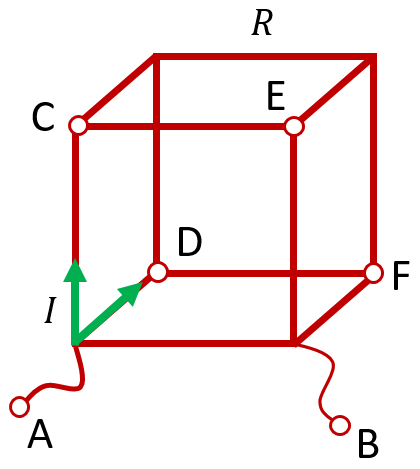
2 4. Two in a cube The cube is assembled from identical resistors with resistance R. Two resistors are replaced with ideal jumpers, as shown in the figure. Find the total resistance of the resulting system between pins A and B. Which of the remaining resistors can be removed without changing the total resistance of the system? If you know that most of the resistors in the circuit carry a current of I = 2 A, calculate the current in the wire connected to node A (or B)? Calculate the current flowing through an ideal jumper AA? 5. Ice spot Determine what maximum mass mn of water vapor, taken at a temperature of 1 C, may be required to heat the ice in the calorimeter to the melting temperature (without melting). The exact mass of ice and its initial temperature are not known, but these values may lie in the area highlighted in the -3 m/m diagram. Specific heat -4 of vaporization L = 2.3 MJ/kg, specific heat of melting of ice λ = 34 kJ/kg, specific heat of water c = 4 2 J/(kg C), specific heat of ice c1 = 2 1 J/(kg WITH). The mass of ice m in the diagram is given in conventional units, showing how many times the mass of ice is less than m = 1 kg. Neglect the heat capacity of the calorimeter and heat loss t, C
3 1st class 1. Power time As a result of the experiment, the dependence of the power N of a constant horizontal force on the time t of its action on a block of mass m = 2 kg initially resting on a smooth horizontal table was obtained. Some measurements may not be very accurate. determine the power of the force at time τ = 6 s; find the value of force F. N, W 1.4 2.8 4.5 5, 6, 1.4 14.7 16.6 18.3 t, s 1, 1.5 2, 2.5 3.2 5 , 7.2 8.4 9, 2. In the hole, Rod AB touches the ledge K of a hemispherical hole of radius R. Point A moves uniformly with speed υ along the surface of the hole, starting from the bottom point N, to point M. Find the dependence of the modulus of speed u of the end rod B from the angle α that the rod makes with the horizon. The length of rod AB is 2R. 3. Water with ice Some water and ice were mixed in the calorimeter. Their exact masses and initial temperatures are unknown, but these values lie in the shaded areas highlighted in the diagram. Find the maximum amount of heat that could be transferred from water to ice if, after thermal equilibrium was established, the mass of ice did not change. Determine the possible mass of the contents of the calorimeter in this case. Specific heat of melting of ice λ = 34 kJ/kg, specific heat of water c = 42 J/(kg C), specific heat of ice c1 = 21 J/(kg C). The masses of water and ice in the diagram are given in conventional units, showing how many times their masses are less than m = 1 kg. Neglect the heat capacity of the calorimeter and heat losses t, C 1 m /m
4 4. Three in a cube The cube is assembled from identical resistors with resistance R. Three resistors were replaced with ideal jumpers, as shown in the figure. Find the total resistance of the resulting system between pins A and B. Which of the remaining resistors can be removed without changing the total resistance of the system? If the current flowing through most of the resistors in an electrical circuit is known to be equal, calculate the current in the wire connected to node A (or B)? I 2A Calculate the current flowing through an ideal jumper AA? 5. Conveyor on its side A conveyor belt lying on its side moves along a rough horizontal floor so that the plane of the belt is vertical. The speed of the conveyor belt is υ. The conveyor moves along the floor at a constant speed u perpendicular to the main sections of its belt. Over some time, the conveyor has moved a distance s. Its new position is shown in the figure. The conveyor pushes a block shaped like rectangular parallelepiped. The figure shows a top view of this system. Neglecting the deflection of the tape and assuming the motion of the block to be steady, find the displacement of the block during the time s/u. Determine the work done by the conveyor to move the block during this time. The coefficient of friction between the block and the floor is μ1, and between the block and the tape is μ2.
5 11th grade 1. Power in space A constant horizontal force F began to act on a block of mass m = 2 kg, initially resting on a smooth horizontal table. As a result, the dependence of the power N on the displacement s of the block was obtained. Some measurements may not be very accurate. In which coordinate axes is the experimental dependence of power on displacement linear? Determine the power of the force at the point with coordinate s = 1 cm. Find the value of the force F. N, W, 28.4.57.75 1.2 1.1 1.23 1.26 1.5 s, cm 1, 2, 4, 7, “Dark Matter” Clusters of stars form collisionless galactic systems in which the stars move uniformly in circular orbits around the axis of symmetry of the system. The NGC 2885 galaxy consists of a cluster of stars in the form of a ball (a core with a radius r = 4 kpc) and a thin ring, the inner radius of which coincides with the radius of the core, and the outer one is equal to 15 r. The ring consists of stars with negligible mass compared to the core. In the core, stars are evenly distributed. It was found that the linear speed of movement of stars in the ring does not depend on the distance to the center of the galaxy: from the outer edge of the ring up to the edge of the core, the speed of stars is υ = 24 km/s. This phenomenon can be explained by the presence of a non-luminous mass (“ dark matter"), distributed spherically symmetrically relative to the center of the galaxy outside its core. 1) Determine the mass Mya of the galactic nucleus. 2) Determine the average density ρ of the matter of the galactic nucleus. 3) Find the dependence of the density of “dark matter” ρт(r) on the distance to the center of the galaxy. 4) Calculate the ratio of the mass of “dark matter”, which influences the motion of stars in the disk, to the mass of the core. Note: 1 kpc = 1 kiloparsec = 3. m, gravitational constant γ = 6. N m 2 kg 2.
6 3. Four in a cube The cube is assembled from identical resistors with resistance R. The four resistors are replaced with ideal jumpers, as shown in the figure. Find the total resistance of the resulting system between contacts A and B. Through which resistors is the current flow maximum, and through which is it minimum? Find these current values if the current entering node A is I = 1.2 A? What is the current flowing through an ideal jumper AA`? 4. Diamond. The cyclic process performed over an ideal gas on the (p, V) plane is a rhombus (see qualitative figure). Vertices (1) and (3) lie on the same isobar, and vertices (2) and (4) lie on the same isochore. During the cycle, the gas has done work A. How different is the amount of heat Q12 supplied to the gas in section 1-2 from the amount of heat Q 3.4 in section 3-4?, removed from the gas in section 5. There are no fluctuations! In an electrical circuit (see Fig.), consisting of a resistor with resistance R, a coil with inductance L, a charge Q is located on a capacitor with capacitance C. At some point in time, switch K is closed and at the same time they begin to change the capacitance of the capacitor so that an ideal voltmeter shows a constant voltage. 1) How does the capacitance of the capacitor C(t) depend on time as t changes from to t 1 C L? 2) How much work was done by external forces during time t1? Consider that t 1 L / R C L. Hint. The amount of heat released by the resistor during time t1 is equal to t1 2 2 Q WR I () t Rdt. 3C
Grade 11 1 Power in space A constant horizontal force F began to act on a block of mass m = kg, initially resting on a smooth horizontal table. As a result, the dependence was obtained
Regional stage All-Russian Olympiad schoolchildren in physics January 16, 11th grade 1 Power in space A block of mass m = kg initially resting on a smooth horizontal table began to act
Regional stage of the All-Russian Olympiad for schoolchildren in physics. January 6, 9th grade. Minimum distance A car traveling at a speed v, at some moment begins to move with such a constant acceleration,
Class 1 1. Time of power As a result of the experiment, the dependence of the power N of a constant horizontal force on the time t of its action on a body initially at rest on a smooth horizontal
Grade 11 1. Density of oxygen Find the density of oxygen at pressure param1 kPa and temperature param2 K. Consider the gas ideal. param1 50 150 200 300 400 param2 300 350 400 450 500 2. Power in the circuit
Grade 7 1. A coil of copper wire has a mass of 360 g. Find the length of the wire in the coil if the cross-sectional area of the wire is 0.126 mm 2, and 1 cm 3 of copper has a mass of 8.94 g. Express the answer in meters and
I. V. Yakovlev Materials on physics MathUs.ru Open Olympiad of the Physics and Technology Lyceum 2015 Physics, grade 11 1. On a thin transparent horizontal table lies a thin collecting lens with a focal length F = 70
The first (qualifying) stage of the academic competition of the Schoolchildren Olympiad “Step into the Future” in the general education subject “Physics”, Autumn 05. Option TASK A. The first half of the time the body moves
9th grade School student Petya Ivanov, from the six wires at his disposal, assembled the circuit shown in Fig. 1. Find the resistance of the circuit between points A and D if the resistances of wires AB and BD are equal
Grade 11. Round 1 1. Problem 1 A cylindrical washer sliding along smooth ice with speed, experienced a frontal elastic collision with a resting cylindrical washer of a different mass. After the collision, the first
Interregional subject Olympiad of the Kazan Federal University in the subject "Physics" 9th grade. Option 1. 2014-2015 academic year, online tour 1. (1 point) Boy Petya the first half of the way from school
I. V. Yakovlev Materials on physics MathUs.ru Phystech Olympiad in physics, grade 11, online stage, 2013/14 1. A stone thrown from the roof of a barn almost vertically upward at a speed of 15 m/s fell to the ground
Bank of tasks in physics 1st grade MECHANICS Uniform and uniformly accelerated rectilinear motion 1 The figure shows a graph of the dependence of the coordinates of a body on time during its straight motion along the x axis.
Olympics named after J. C. Maxwell Regional Stage January 6, 7th grade. Where is the density here? The laboratory measured the mass and volume of five bodies made of four materials: birch, ρ B =.7
Repeat paragraphs 88-93 perform exercise 12. Perform the test Option 3679536 1. Task 1 The figure shows graphs of the modulus of the speed of movement of four cars versus time. One of
Minsk City Olympiad PHYSICS 2002, 11th grade. 1. The rotor of the electric motor model is a rectangular frame with area S, containing n turns of wire, mounted on a massive base,
Ministry of Education and Science of the Perm Territory Physics Assignments municipal stage All-Russian Olympiad for schoolchildren in the Perm region 2017/2018 academic year METHODOLOGICAL RECOMMENDATIONS FOR CONDUCTING THE MUNICIPAL
MOSCOW OLYMPIAD FOR SCHOOLCHILDREN IN PHYSICS 2016 2017 academic year. ZERO ROUND, CORRESPONDENCE ASSIGNMENT. 11TH GRADE The attached file contains the November correspondence assignment for the 11th grade. Prepare several sheets
Grade 10. Option 1. 1. (1 point) The rotational speed of a light-engine aircraft propeller is 1500 rpm. How many revolutions will the propeller have time to make on a path of 90 km at a flight speed of 180 km/h? 1) 750 2) 3000 3)
Physics. For calculations, take: m Gravity acceleration g 10 s Universal gas constant J R 8.31 mol K Avogadro's constant N A 6.0 10 mol 3 1 Planck's constant h 34 6.63 10 J s 1 F Electric
MOSCOW STATE TECHNICAL UNIVERSITY NAMED AFTER NE BAUMAN FINAL STAGE OF THE OLYMPIAD “STEP INTO THE FUTURE” IN THE COMPLEX OF SUBJECTS “Engineering and Technology” OPTION 8 TASK From point A, located
Kurchatov 2018, physics, qualifying stage 11th grade Hydrostatics Problem 1.1 A cube with side a = 10 cm floats in mercury, immersed in 1/4 of its volume. Water is gradually added on top of the mercury until
The final (in-person) stage of the All-Siberian Olympiad in Physics Problems of grade 9. (March 29, 2009) 2R m 3R 1. A massive homogeneous chain with a load of mass m at one end is thrown over a block of radius R and is located
The attached file contains the November correspondence assignment for the 11th grade. Prepare several squared sheets of paper on which you will handwrite detailed solutions to the attached problems. Take a photo of the pages
The first (qualifying) stage of the academic competition of the Schoolchildren Olympiad “Step into the Future” in the general education subject “Physics”, autumn 016. Option 1 1. The disk rolls without slipping on a horizontal
Rigid body dynamics. 1. A thin homogeneous rod AB of mass m = 1.0 kg moves translationally with acceleration a = 2.0 m/s 2 under the influence of forces F 1 and F 2. Distance b = 20 cm, force F 2 = 5.0 N. Find the length
9F Section 1. Concepts, definitions Insert the missing words: 1.1 A body can be considered a material point only when 1.2 If at any moment of time all points of the body move equally, then such
I. V. Yakovlev Materials on physics MathUs.ru Open Olympiad of the Physics and Technology Lyceum 2015 Physics, grade 9 1. Mass of a test tube filled to the brim with water M 1 = 160 g. After a piece of metal was placed in it
I. V. Yakovlev Materials on physics MathUs.ru Gravity Problem 1. (MIPT, 1987) At what speed would an airplane have to fly along the equator so that the pressure force of seated passengers on the airplane seats decreases
Final annual test in physics, grade 10, option 1 Part A A1. On a ring road of length L = 15 km, a truck and a motorcycle are traveling in one direction at speeds V1, respectively.
SCHOOL OLYMPIADS “STEP INTO THE FUTURE” Complex of subjects “Engineering and technology” OLYMPIAD TASK MATERIALS 008-009 YEAR I. Scientific and educational competition MATHEMATICS TASKS Solve a system of equations
Lesson 11 Final 2. Mechanics. Task 1 The figure shows a graph of the cyclist’s path S as a function of time t. Determine the time interval after the start of movement when the cyclist was moving with
Class 11 Ticket 11-01 Code 1. A system of three bars located on a horizontal table is set in motion by applying a horizontal force F (see figure). Friction coefficient between table and bars
Physics, 9th grade (10th grade - 1st half-year) Option 1 1 Using the graph of the modulus of velocity versus time presented in the figure, determine the modulus of acceleration of a rectilinearly moving body at the moment of time
Deferred tasks (25) In the region of space where a particle with a mass of 1 mg and a charge of 2 10 11 C is located, a homogeneous horizontal electric field. What is the strength of this field if
Minsk regional Olympiad for schoolchildren in physics 2000, 11th grade. 1. Two washers of masses m and 2m, connected by a weightless thread of length l, lie on a smooth horizontal surface so that the thread is completely stretched.
9th grade Problem. Icicle falling. An icicle came off the roof of the house and in t=0.2 s flew past a window whose height h =.5 m. From what height h x, relative to the top edge of the window, did it come off? Dimensions
I. V. Yakovlev Materials on physics MathUs.ru Open Olympiad of the Physics and Technology Lyceum 2015 Physics, grade 10 1. A sealed vessel is divided into two compartments with a heat-insulating partition, in which a small
Grade 10. Option 1 1. A body slides down an inclined plane with an angle of inclination = 30 o. At the first k=1/3 of the path, the friction coefficient is 1 05. Determine the coefficient of friction on the remaining section of the path if at the base
Option 2805281 1. A boy rides a sled at uniform acceleration down a snowy hill. The speed of the sled at the end of the descent is 10 m/s. The acceleration is 1 m/s 2, the initial speed is zero. What is the length of the slide? (Give me the answer
Tula State University. Physics Olympiad February 6. A cylinder of radius R = cm is sandwiched between two horizontal surfaces that move in different directions at speeds v = 4 m/s
ALL-RUSSIAN OLYMPID FOR SCHOOLCHILDREN IN PHYSICS. 017 018 school MUNICIPAL ETP. 10 CLSS 1. Two balls are thrown simultaneously towards each other with the same initial speeds: one from the surface of the earth
Administrative work for the 1st half of the year Option 1. Part 1 A1. The graph shows the dependence of the speed of a rectilinearly moving body on time. Determine the acceleration modulus of the body. 1) 10 m/s 2 2) 5 m/s
The first (qualifying) stage of the academic competition of the Schoolchildren Olympiad “Step into the Future” in the educational subject “physics”, autumn 05 Option 5 TASK The body performs two consecutive, identical
Olympic tasks 2014/2015 academic year Grade 9 Option 1 1. A cube of density ρ 1 is held in equilibrium by a weightless spring under an inclined wall, the angle of inclination of which is equal to α, in a liquid of density ρ 2 >ρ
Year 216 Class 9 Ticket 9-1 1 Two weights of masses m and, located on a smooth horizontal table, are connected by a thread and connected to a load of mass 3m by another thread thrown over a weightless block (see figure) By friction
A typical version of the academic competition of the Olympiad for schoolchildren “Step into the Future” in the general education subject “Physics” TASK 1. A point moves along the x axis according to the law of point velocity at t = 1 s.
Task 1 A cylindrical vessel into which liquid was poured was closed with a sealed lid and began to move vertically downward with an acceleration of 2.5 g. Determine the pressure of the liquid on the lid of the vessel, if stationary
2.1. There was ice in the calorimeter at a temperature t 1 = -5 C. What was the mass m 1 of ice if, after adding t 2 = 4 kg of water having a temperature t 2 = 20 C to the calorimeter, and establishing thermal equilibrium
MOSCOW STATE TECHNICAL UNIVERSITY NAMED AFTER NE BAUMAN FINAL STAGE OF THE OLYMPIAD “STEP INTO THE FUTURE” IN THE COMPLEX OF SUBJECTS “Engineering and Technology” OPTION 5 TASK From point A, located
Ticket N 5 Ticket N 4 Question N 1 A horizontal force begins to act on a body of mass m 2.0 kg, the modulus of which linearly depends on time: F t, where 0.7 N/s. Friction coefficient k 0.1. Define the moment
Establishing correspondence, part 2 1. a stick located on a rough horizontal surface begins to move uniformly accelerated under the influence of a force in the reference frame associated with the horizontal surface,
Complex Olympiad for schoolchildren "Akademika" [email protected] 1. The initial speed of a stone thrown at a certain angle to the horizontal is 10 m/s, and after a time of 0.5 s the speed of the stone is 7 m/s. On
Task 1 Choose the orientation of the image of the object “b” in the plane mirror “a” (see figure). a 45 0 b a b c d e Task 2 An amount of heat Q was transferred to a body of mass m and specific heat capacity c. Temperature
Ticket N 5 Ticket N 4 Question N 1 Two bars with masses m 1 = 10.0 kg and m 2 = 8.0 kg, connected by a light inextensible thread, slide along an inclined plane with an angle of inclination = 30. Determine the acceleration of the system.
Republican Subject Olympiad District (City) stage Physics First Name Last Name School 1 Duration of the exam is 180 minutes 4 incorrect answers take points for 1 correct answer 3 Each question
Belarusian Republican Olympiad in Physics (Gomel, 1998) Grade 9 9.1 To study the elastic properties of rubber, a rubber band was suspended vertically, and various
Part 1 The answers to tasks 1 4 are a number, a number or a sequence of numbers. Write the answer in the answer field in the text of the work, and then transfer it to ANSWER FORM 1 to the right of the number of the corresponding task,
Tasks B2 in physics 1. A spring pendulum was taken out of its equilibrium position and released without an initial speed. How do the following physical factors change during the first quarter of the period of oscillation of the pendulum's weight?
Phystech Olympiad in Physics 9th Grade Ticket - Code (to be filled in by the secretary) 3. The cannon is installed on a flat mountain slope forming an angle with the horizon. When fired “up” a slope, the projectile falls onto the slope
Phystech Olympiad in Physics Grade 8 Ticket - Code (filled in by the secretary) A system of three bars located on a horizontal table is set in motion by applying a horizontal force (see figure) Coefficient
1 Kinematics 1 The material point moves along the x axis so that the time coordinate of the point x(0) B Find x (t) V x At At the initial moment The material point moves along the x axis so that ax A x At the initial
Lesson 7 Laws of Conservation Task 1 The figure shows graphs of changes in the velocities of two interacting carts of different masses (one cart catches up and pushes the other). What information about carts
Explanation of the phenomena 1. The figure shows a schematic view of a graph of changes in the kinetic energy of a body over time. Choose two true statements that describe the movement in accordance with the given
I. V. Yakovlev Materials on physics MthUs.ru Electromagnetic induction Problem 1. A wire ring of radius r is in a uniform magnetic field, the lines of which are perpendicular to the plane of the ring. Induction
9th grade. Option 1. The body was thrown horizontally from the tower. After t = s its speed increased by k=3 times. At what speed V0 was the body thrown? The speed of a body changes depending on time as For a given
Grade 7 1. How many times a day do the hour and minute hands of a clock lie on the same straight line? 2. The mass of an empty canister is 200 g, and a canister filled with kerosene is 5 kg. How many liters of kerosene are in a canister?
I. V. Yakovlev Materials on physics MathUs.ru Contents Friction force 1 All-Russian Olympiad for schoolchildren in physics................... 1 2 Moscow Physics Olympiad...... .................... 3 3 MIPT
Results of the municipal stage of the All-Russian Olympiad for schoolchildren in physics 2012-2013 academic year Analysis of the results of the municipal stage of the Olympiad 1 task. 9th grade Experimenter Gluck is watching from the balcony
Instructions for tasks #1_45: These tasks ask questions and give five possible answers, only one of which is correct. Find the number corresponding to this task in the answer sheet, find
Solutions and evaluation criteria Problem 1 A wooden cylinder floats in a cylindrical vessel filled with water, as shown in Fig. 1, protruding a = 60 mm above the liquid level, which is equal to h 1 = 300 mm. To the top
LYCEUM 1580 (AT MSTU NAMED AFTER N.E. BAUMAN) DEPARTMENT OF “FUNDAMENTALS OF PHYSICS”, 11TH GRADE, 3rd SEMESTER 2018-2019 ACADEMIC YEAR Option 0 Problem 1. Fine weeding ring with area S = 100 cm 2 -, having resistance R = 0 .01
Goals: educational: systematize students’ knowledge and skills in solving problems and calculating equivalent resistances using models, frames, etc.
Developmental: development of logical thinking skills, abstract thinking, skills to replace equivalence schemes, simplify the calculation of schemes.
Educational: fostering a sense of responsibility, independence, and the need for skills acquired in class in the future
Equipment: wire frame of a cube, tetrahedron, mesh of an endless chain of resistance.
DURING THE CLASSES
Update:
1. Teacher: “Let’s remember the series connection of resistances.”
Students draw a diagram on the board.
and write down
U rev =U 1 +U 2
Y rev =Y 1 =Y 2
Teacher: remember the parallel connection of resistances.
A student sketches a basic diagram on the board:
Y rev =Y 1 =Y 2
; for for n equal
Teacher: Now we will solve problems on calculating the equivalent resistance. A section of the circuit is presented in the form of a geometric figure or a metal mesh.
Task No. 1
A wire frame in the form of a cube, the edges of which represent equal resistances R. Calculate the equivalent resistance between points A and B. To calculate the equivalent resistance of a given frame, it is necessary to replace it with an equivalent circuit. Points 1, 2, 3 have the same potential, they can be connected into one node. And points (vertices) of the cube 4, 5, 6 can be connected into another node for the same reason. Students have such a model on each desk. After completing the described steps, draw an equivalent circuit.

In the AC section the equivalent resistance is ; on CD; on DB; and finally for the series connection of resistances we have: ![]()
By the same principle, the potentials of points A and 6 are equal, B and 3 are equal. Students combine these points on their model and get an equivalent diagram:

Calculating the equivalent resistance of such a circuit is simple ![]()
Problem No. 3
The same model of a cube, with inclusion in the circuit between points 2 and B. Students connect points with equal potentials 1 and 3; 6 and 4. Then the diagram will look like this:

Points 1,3 and 6,4 have equal potentials, and no current will flow through the resistances between these points and the circuit is simplified to the form; the equivalent resistance of which is calculated as follows:


Problem No. 4

An equilateral triangular pyramid, the edge of which has a resistance R. Calculate the equivalent resistance when connected to the circuit.
Points 3 and 4 have equal potential, so no current will flow along edge 3.4. The students clean it up.
Then the diagram will look like this:



The equivalent resistance is calculated as follows:
Problem No. 5

Metal mesh with link resistance equal to R. Calculate the equivalent resistance between points 1 and 2.
At point 0 you can separate the links, then the diagram will look like:

![]() - the resistance of one half is symmetrical at 1-2 points. There is a similar branch parallel to it, so
- the resistance of one half is symmetrical at 1-2 points. There is a similar branch parallel to it, so ![]()
Problem No. 6

The star consists of 5 equilateral triangles, the resistance of each ![]() .
.
Let's consider a classic problem. Given a cube, the edges of which represent conductors with some identical resistance. This cube is included in an electrical circuit between all its possible points. Question: what is equal cube resistance in each of these cases? In this article, a physics and mathematics tutor talks about how this classic problem is solved. There is also a video tutorial in which you will find not only a detailed explanation of the solution to the problem, but also a real physical demonstration confirming all the calculations.
So, the cube can be connected to the circuit in three different ways.
Resistance of a cube between opposite vertices
In this case, the current, having reached the point A, is distributed between three edges of the cube. Moreover, since all three edges are equivalent in terms of symmetry, no edge can be given more or less “significance”. Therefore, the current between these edges must be distributed equally. That is, the current strength in each edge is equal to:

The result is that the voltage drop across each of these three edges is the same and is equal to , where is the resistance of each edge. But the voltage drop between two points is equal to the potential difference between these points. That is, the potentials of the points C, D And E are the same and equal. For symmetry reasons, the point potentials F, G And K are also the same.
Points with the same potential can be connected by conductors. This will not change anything, because no current will flow through these conductors anyway:

As a result, we find that the edges A.C., AD And A.E. T. Likewise the ribs FB, G.B. And K.B. connect at one point. Let's call it a point M. As for the remaining 6 edges, all their “beginnings” will be connected at the point T, and all ends are at the point M. As a result, we get the following equivalent circuit:

![]()
Resistance of a cube between opposite corners of one face
In this case, the equivalent edges are AD And A.C.. The same current will flow through them. Moreover, equivalent are also KE And KF. The same current will flow through them. Let us repeat once again that the current between equivalent edges must be distributed equally, otherwise the symmetry will be broken:

Thus, in this case the points have the same potential C And D, as well as points E And F. This means that these points can be combined. Let the points C And D unite at a point M, and the points E And F- at the point T. Then we get the following equivalent circuit:

On a vertical section (directly between the points T And M) no current flows. Indeed, the situation is similar to a balanced measuring bridge. This means that this link can be excluded from the chain. After this, calculating the total resistance is not difficult:

The resistance of the upper link is equal to , the resistance of the lower link is . Then the total resistance is:
![]()
Resistance of a cube between adjacent vertices of the same face
This is the last possible variant connecting the cube to an electrical circuit. In this case, the equivalent edges through which the same current will flow are the edges A.C. And AD. And, accordingly, points will have identical potentials C And D, as well as points symmetric to them E And F:
We again connect points with equal potentials in pairs. We can do this because no current will flow between these points, even if we connect them with a conductor. Let the points C And D unite into a point T, and the points E And F- exactly M. Then we can draw the following equivalent circuit:

The total resistance of the resulting circuit is calculated using standard methods. We replace each segment of two parallel-connected resistors with a resistor with resistance . Then the resistance of the “upper” segment, consisting of series-connected resistors , and , is equal to .
This segment is connected to the “middle” segment, consisting of one resistor with a resistance of , in parallel. The resistance of a circuit consisting of two parallel-connected resistors with resistance and is equal to:
That is, the scheme is simplified to an even simpler form:

As you can see, the resistance of the “upper” U-shaped segment is equal to:
![]()
Well, the total resistance of two parallel connected resistors is equal to:
Experiment to measure the resistance of a cube
To show that all this is not a mathematical trick and that there is real physics behind all these calculations, I decided to conduct a direct physical experiment to measure the resistance of a cube. You can watch this experiment in the video at the beginning of the article. Here I will post photos of the experimental setup.
Especially for this experiment, I soldered a cube whose edges were identical resistors. I also have a multimeter that I turned on in resistance mode. The resistance of a single resistor is 38.3 kOhm:

Goals: educational: systematize students’ knowledge and skills in solving problems and calculating equivalent resistances using models, frames, etc.
Developmental: development of logical thinking skills, abstract thinking, skills to replace equivalence schemes, simplify the calculation of schemes.
Educational: fostering a sense of responsibility, independence, and the need for skills acquired in class in the future
Equipment: wire frame of a cube, tetrahedron, mesh of an endless chain of resistance.
DURING THE CLASSES
Update:
1. Teacher: “Let’s remember the series connection of resistances.”
Students draw a diagram on the board.
and write down
U rev =U 1 +U 2
Y rev =Y 1 =Y 2
Teacher: remember the parallel connection of resistances.
A student sketches a basic diagram on the board:
Y rev =Y 1 =Y 2
; for for n equal
Teacher: Now we will solve problems on calculating the equivalent resistance. A section of the circuit is presented in the form of a geometric figure or a metal mesh.
Task No. 1
A wire frame in the form of a cube, the edges of which represent equal resistances R. Calculate the equivalent resistance between points A and B. To calculate the equivalent resistance of a given frame, it is necessary to replace it with an equivalent circuit. Points 1, 2, 3 have the same potential, they can be connected into one node. And points (vertices) of the cube 4, 5, 6 can be connected into another node for the same reason. Students have such a model on each desk. After completing the described steps, draw an equivalent circuit.

In the AC section the equivalent resistance is ; on CD; on DB; and finally for the series connection of resistances we have: ![]()
By the same principle, the potentials of points A and 6 are equal, B and 3 are equal. Students combine these points on their model and get an equivalent diagram:

Calculating the equivalent resistance of such a circuit is simple ![]()
Problem No. 3
The same model of a cube, with inclusion in the circuit between points 2 and B. Students connect points with equal potentials 1 and 3; 6 and 4. Then the diagram will look like this:

Points 1,3 and 6,4 have equal potentials, and no current will flow through the resistances between these points and the circuit is simplified to the form; the equivalent resistance of which is calculated as follows:


Problem No. 4

An equilateral triangular pyramid, the edge of which has a resistance R. Calculate the equivalent resistance when connected to the circuit.
Points 3 and 4 have equal potential, so no current will flow along edge 3.4. The students clean it up.
Then the diagram will look like this:



The equivalent resistance is calculated as follows:
Problem No. 5

Metal mesh with link resistance equal to R. Calculate the equivalent resistance between points 1 and 2.
At point 0 you can separate the links, then the diagram will look like:

![]() - the resistance of one half is symmetrical at 1-2 points. There is a similar branch parallel to it, so
- the resistance of one half is symmetrical at 1-2 points. There is a similar branch parallel to it, so ![]()
Problem No. 6

The star consists of 5 equilateral triangles, the resistance of each ![]() .
.
Between points 1 and 2, one triangle is parallel to four triangles connected in series

Having experience in calculating the equivalent resistance of wire frames, you can begin to calculate the resistance of a circuit containing an infinite number of resistances. For example:

If you separate the link

from the general circuit, then the circuit will not change, then it can be represented in the form

 or
or ![]() ,
,
solve this equation for R eq.

Lesson summary: we learned to abstractly represent circuit diagrams of circuit sections and replace them with equivalent circuits, which make it easy to calculate the equivalent resistance.

Instructions: This model can be represented as:

Are you so familiar with Ohm’s law (connections of conductors)? // Quantum. - 2012. - No. 1. - P. 32-33.
By special agreement with the editorial board and editors of the journal "Kvant"
The currents continue indefinitely at a constant rate, ... but they always stop the moment the circuit is broken.
Andre Ampere
The transition of electricity between two nearby elements, other things being equal, is proportional to the difference in electroscopic forces in these elements.
Georg Ohm
If given a system n conductors that are arbitrarily connected to each other, and an arbitrary electromotive force is applied to each conductor, then the required number of linear equations for determining the currents flowing through the conductors can be obtained using... two theorems.
Gustav Kirchhoff
...by translating the essential features of real circuit elements into the language of idealizations, it is possible to analyze an electrical circuit relatively simply.
Richard Feynman
Our first meetings with electrical diagrams happen when we plug in household appliances at home or come across an intricacy of wiring under the cover of some electronic device or when we notice power lines on high supports and thick wires along which the current collectors of electric trains, trolleybuses and trams slide. Later we draw diagrams at school, perform simple experiments and learn about the laws of electrical, primarily direct, current, flowing - how could it be otherwise! - by wire.
But at the same time we use mobile phones, wireless local networks, “we are stuck in the air” to connect to the Internet, and we increasingly hear that wireless transmission of not only information, but also electricity is just around the corner. How archaic then will all these bulky circuits, wires, terminals, rheostats and the laws describing them seem!
Take your time. Firstly, no matter what we transmit - signals or energy, there are emitters and receivers that will not operate without currents flowing through the conductors stuffed into them. Secondly, not everything can be miniaturized, for example, transport or power plants. Therefore, we have to deal with electrical networks, and therefore with the connections of the conductors itself. different types I'll have to deal with it for a long time. We will continue this topic in the next issue of Kaleidoscope, at the end of which we will place a general list of “Quantum” publications on the topic “Ohm’s Law”.
Questions and tasks
1. Why can birds perch safely on high voltage wires?
2. A garland is assembled from series-connected light bulbs for a flashlight, designed to be connected to a 220 V network. Each light bulb has a voltage of only about 3 V, but if you unscrew one of the light bulbs from the socket and put your finger in it, it will “jerk” strongly. . Why?
3. The battery is closed by three conductors of equal length connected in series. Figure 1 shows a graph showing the voltage drop across them. Which conductor has the highest and which has the least resistance?
4. Calculate the total resistance of the circuit shown in Figure 2 if R= 1 Ohm.

5. Five conductors of equal resistance were connected so that, under the influence of a total voltage of 5 V, the current in the circuit turned out to be equal to 1 A. Determine the resistance of one conductor. Does the problem have a single solution?
6. From identical resistors with a resistance of 10 Ohms, you need to create a circuit with a resistance of 6 Ohms. What is the smallest number of resistors needed for this? Draw a diagram of the circuit.
7. Give an example of a circuit that is not a combination of series and parallel connections.
8. How will the resistance of a circuit consisting of five identical conductors change? r each, if we add two more of the same conductors, as shown by the dashed lines in Figure 3?

9. What is the resistance R of each of two identical resistors (Fig. 4), if the voltmeter has a resistance R V= 3 kOhm when switched on according to schemes a) and b) shows the same voltage? The voltage in the circuit is the same in both cases.

10. An electrical circuit consisting of resistors with resistances R 1, R 2 and R 3 is connected to two constant voltage sources U 1 and U 2, as shown in Figure 5. Under what conditions will the current through the resistor with resistance R 1 be zero?

11. Find the resistance of the “star” (Fig. 6) between points A and B, if the resistance of each link is equal r.

12. A hollow cube was soldered from thin homogeneous sheets of tin, and conductors were soldered to the two opposite vertices of the large diagonal, as shown in Figure 7. The resistance of the cube between these conductors turned out to be 7 Ohms. Find the strength of the electric current crossing edge AB of the cube if the cube is connected to a 42 V source.

13. Determine the currents in each side of the cell shown in Figure 8, the total current from node A to node B, and the total resistance between these nodes. Each side of the cell has a resistance r, and the current flowing along the indicated side is equal to i.

14. Two jumpers CE and DF were soldered into an electrical circuit consisting of six identical resistors with resistance R, as shown in Figure 9. What was the resistance between terminals A and B?

15. The galvanic element is closed into two parallel conductors with resistances R 1 and R 2. Will the currents in these conductors decrease if their resistance is increased?
Microexperience
How can you determine the length of insulated copper wire rolled into a large coil without unwinding it?
It's interesting that...
Ohm's experiments, which seem trivial today, are remarkable in that they marked the beginning of clarifying the root causes of electrical phenomena, which for a little less than two hundred years remained very vague and devoid of any experimental justification.
Not being familiar with Ohm's law, the French physicist Pouille, through experimentation, came to similar conclusions in 1837. Having learned that the law had been discovered a decade ago, Pouille set about thoroughly checking it. The law was confirmed with high accuracy, and a “by-product” was the study of Ohm’s law by French schoolchildren until the 20th century under the name of Pouillet’s law.
... when deducing his law, Ohm introduced the concepts of “resistance”, “current strength”, “voltage drop” and “conductivity”. Along with Ampere, who introduced the terms “ electrical circuit" and "electric current" and determined the direction of current in a closed circuit, Ohm laid the foundation for further electrodynamic research on the path to the practical use of electricity.
...in 1843, the English physicist Charles Wheatstone, using Ohm's law, invented a method for measuring resistance, now known as the Wheatstone bridge.
...the identity of the “electroscopic forces” included in the formulation of Ohm’s law with electric potentials was proven by Kirchhoff. Somewhat earlier, he had established the laws of current distribution in branched circuits, and later constructed general theory movement of current in conductors, assuming the existence in them of two equal counter flows of positive and negative electricity.
...the intensive development of electrical measurement methods in the 19th century was facilitated by technical demands: the creation of overhead telegraph lines, the laying of underground cables, the transmission of electric current through uninsulated overhead wires and, finally, the construction of an underwater transatlantic telegraph. The theorist of the last project was the outstanding English physicist William Thomson (Lord Kelvin).
...some practical problems of economics and logistics, such as finding the minimum cost distribution of goods, found their solution when modeling transport flows using electrical networks.
Questions and tasks
1. The resistance of the bird’s body is much greater than the resistance of the section of wire parallel to it between its legs, therefore the current strength in the bird’s body is small and harmless.
2. The finger has a very high resistance compared to the resistance of the light bulb. When it is “turned on” in series with the light bulbs, the same current flows through the finger and the light bulbs, so the voltage drop across the finger will be significantly greater than the voltage drop across the light bulbs, i.e. Almost all the mains voltage will be applied to the finger.
3. Conductor 3 has the highest resistance, conductor 2 has the least.
4. Rtot = R = 1 Ohm.
5. When five conductors are connected in series, the resistance of each conductor is R = 1 Ohm. Another solution is possible: the conductors are connected in parallel to each other into 2 groups, one of which has 3 conductors, the other - 2, and these groups are connected to each other in series. Then R = 6 Ohm.
6. Four resistors; see fig. 10.

7. Figure 11 shows the so-called bridge circuit, when currents flow through all resistors.





